题目内容
20. 已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条
已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条对称轴.
(1)求函数f(x)的解析式;
(2)求函数f(-x)的单调增区间;
(3)作出函数f(x)在x∈[0,π]上的图象简图(列表,画图).
分析 (1)利用正弦函数的对称性可得2×$\frac{π}{6}$+ϕ=kπ+$\frac{π}{2}$,k∈Z,又0<ϕ<$\frac{π}{2}$,可求ϕ,即可解得函数解析式;
(2)先求函数解析式f(-x)=-sin(2x-$\frac{π}{6}$),由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,即可解得函数f(x)的增区间.
(3)用五点法即可作图得解.
解答 解:(1)∵$x=\frac{π}{6}$是函数f(x)=sin(2x+ϕ)$(0<ϕ<\frac{π}{2})$图象的一条对称轴.
∴2×$\frac{π}{6}$+ϕ=kπ+$\frac{π}{2}$,k∈Z.
∴ϕ=kπ+$\frac{π}{6}$,k∈Z.
又0<ϕ<$\frac{π}{2}$,
∴ϕ=$\frac{π}{6}$,
∴可得:$f(x)=sin(2x+\frac{π}{6})$;
(2)∵f(-x)=sin(-2x+$\frac{π}{6}$)=-sin(2x-$\frac{π}{6}$),
∴由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,即可解得函数f(x)的增区间为$[kπ+\frac{π}{3},kπ+\frac{5}{6}π],k∈Z$.
(3)列表
| x | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | π |
| $2x+\frac{π}{6}$ | $\frac{π}{6}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{13π}{6}$ |
| f(x) | $\frac{1}{2}$ | 1 | 0 | -1 | 0 | $\frac{1}{2}$ |

点评 本题主要考查了正弦函数的单调性和对称性,考查了五点法作函数y=Asin(ωx+φ)的图象,属于基本知识的考查.

练习册系列答案
相关题目
11.直线l1:3mx+8y+3m-10=0过定点( )
| A. | (-1,-$\frac{4}{5}$) | B. | (-1,$\frac{4}{5}$) | C. | (-1,$\frac{5}{4}$) | D. | (-1,-$\frac{5}{4}$) |
5.要得到余弦曲线y=cosx,只需将正弦曲线y=sinx向左平移( )
| A. | $\frac{π}{2}$个单位 | B. | $\frac{π}{3}$个单位 | C. | $\frac{π}{4}$个单位 | D. | $\frac{π}{6}$个单位 |
12.如图,在正方体ABCD-A1B1C1D1中,M为棱D1C1的中点.设AM与平面BB1D1D的交点为O,则( )
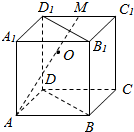

| A. | 三点D1,O,B共线,且OB=2OD1 | B. | 三点D1,O,B不共线,且OB=2OD1 | ||
| C. | 三点D1,O,B共线,且OB=OD1 | D. | 三点D1,O,B不共线,且OB=OD1 |