题目内容
已知f(x-1)=x2,则f(x)的解析式为( )
| A、f(x)=x2-2x-1 |
| B、f(x)=x2-2x+1 |
| C、f(x)=x2+2x-1 |
| D、f(x)=x2+2x+1 |
考点:二次函数的性质
专题:函数的性质及应用
分析:本题可以利用换元法求函数的解析式,得到本题结论.
解答:
解:∵f(x-1)=x2,
令x-1=t,则x=t+1,
∴f(t)=(t+1)2,
∴f(x)=x2+2x+1.
故选D.
令x-1=t,则x=t+1,
∴f(t)=(t+1)2,
∴f(x)=x2+2x+1.
故选D.
点评:本题考查了函数解析式的求法,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m∥n,m⊥α,n?β,则α⊥β |
| C、若m∥α,m∥β,则α∥β |
| D、若m∥α,α⊥β,则m⊥β |
下列结论中是错误命题的是( )
| A、命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0” | ||||
| B、若¬p是q的必要条件,则p是¬q的充分条件 | ||||
C、“M>N”是“(
|
若关于x的方程|x2-2x-3|-m+5=0有4个根,则m的取值范围为( )
| A、(5,9) |
| B、[5,9] |
| C、(-1,3) |
| D、[-1,3] |
 如图,在正方形ABCD中,E为AB的中点,P为线段BD上的任意一点,设向量
如图,在正方形ABCD中,E为AB的中点,P为线段BD上的任意一点,设向量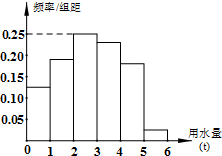 某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表: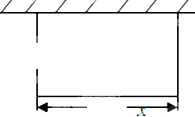 某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.