题目内容
已知f（x+1）的定义域为[1，3]，则
的定义域为（ ）
| f(3-x) | ||
|
| A、[-3，-1] |
| B、（0，1] |
| C、[1，3] |
| D、[-1，0） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由f（x+1）的定义域求出f（x）的定义域，进一步求出f（3-x）的定义域，结合|x|-x＞0求得x的取值集合得答案．
解答：
解：∵f（x+1）的定义域为[1，3]，即1≤x≤3，得2≤x+1≤4，
函数f（x）的定义域为[2，4]，
由2≤3-x≤4，得-1≤x≤1．
即函数f（3-x）的定义域为[-1，1]．
再由|x|-x＞0，得x＜0．
∴
的定义域为[-1，0）．
故选：D．
函数f（x）的定义域为[2，4]，
由2≤3-x≤4，得-1≤x≤1．
即函数f（3-x）的定义域为[-1，1]．
再由|x|-x＞0，得x＜0．
∴
| f(3-x) | ||
|
故选：D．
点评：本题考查了函数的定义域及其求法，关键是掌握该类问题的解决方法，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
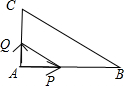在△ABC中，∠B=30°，∠C=60°，AC=1，动点P，Q同时从A出发，沿周界运动，点P沿A→B→C；动点Q沿A→C→B运动到相遇时停止，动点Q的速度是动点P的运动速度的3倍，AP=x，△APQ的面积为y，求函数y=f（x）的解析式，并确定PQ在什么位置时S最大．在等差数列{an}中，若a3+2a6+a9=120，则S11等于（ ）
| A、330 | B、340 |
| C、360 | D、380 |