题目内容
某校开设A类课3门,B类课5门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有
( )
( )
| A、15种 | B、30种 |
| C、45种 | D、90种 |
考点:排列、组合及简单计数问题
专题:排列组合
分析:两类课程中各至少选一门,包含两种情况:A类选修课选1门,B类选修课选2门;A类选修课选2门,B类选修课选1门,写出组合数,根据分类计数原理得到结果.
解答:
解:可分以下2种情况:①A类选修课选1门,B类选修课选2门,有C31C52种不同的选法;
②A类选修课选2门,B类选修课选1门,有C32C51种不同的选法.
∴根据分类计数原理知不同的选法共有C31C52+C32C51=30+15=45种.
故选:C.
②A类选修课选2门,B类选修课选1门,有C32C51种不同的选法.
∴根据分类计数原理知不同的选法共有C31C52+C32C51=30+15=45种.
故选:C.
点评:本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想.本题也可以从排列的对立面来考虑,写出所有的减去不合题意的,可以这样解:C83-C33-C53=45.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,e4) |
| D、(e4,+∞) |
已知函数y=f(x)是R上的减函数,且函数y=f(x-1)的图象关于点A(1,0)对称.设动点M(x,y),若实数x,y满足不等式 f(x2-8y+24)+f(y2-6x)≥0恒成立,则
•
的取值范围是( )
| OA |
| OM |
| A、(-∞,+∞) |
| B、[-1,1] |
| C、[2,4] |
| D、[3,5] |
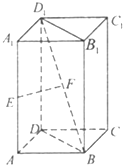 如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.
如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.