题目内容
某校为了解高一年段学生的体重情况,先按性别分层抽样获取样本,再从样本中提取男、女生体重数据,最后绘制出如下图表.已知男生体重在[50,62)的人数为45.
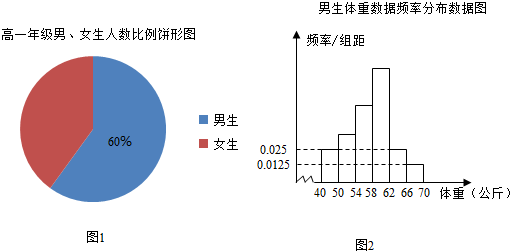
(Ⅰ)根据以上图表,计算体重在[56,60)的女生人数x的值;
(Ⅱ)若从体重在[66,70)的男生和体重在[56,60)的女生中选取2人进行复查,求男、女生各有一人被选中的概率;
(Ⅲ)若体重在[50,54),[54,58),[58,62)的男生人数比为3:5:7,试估算高一年段男生的平均体重.

| 女生体重数据频数分布表 | ||||||
| 体重(公斤) | [36,40) | [40,44) | [44,48) | [48,52) | [52,56) | [56,60) |
| 频数 | 2 | 18 | 10 | 5 | 3 | x |
(Ⅱ)若从体重在[66,70)的男生和体重在[56,60)的女生中选取2人进行复查,求男、女生各有一人被选中的概率;
(Ⅲ)若体重在[50,54),[54,58),[58,62)的男生人数比为3:5:7,试估算高一年段男生的平均体重.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ)利用男生体重数据频率分布直方图,直接求解体重落在区间[50,62)的频率,得到男生体重在[50,62)的人数,按性别分层抽样,根据饼图描述的男,女生人数比,求出体重落在区间[56,60]的女生人数.(Ⅱ)体重落在区间[66,70]的男生人数.记体重落在[66,70]的3名男生为A,B,C,体重落在[56,60]的2名女生为a,b.列出所有基本事件个数.记“男、女生各有一人被选中”的事件为R的数目,利用古典概率模型求解即可.
(Ⅲ)利用体重在[50,54),[54,58),[58,62)的男生人数比为3:5:7,推出男生第2,3,4组体重数据的频率分别为0.15,0.25,0.35,男生第1,5,6组体重数据的频率.即可估计高一年段男生平均体重.
(Ⅲ)利用体重在[50,54),[54,58),[58,62)的男生人数比为3:5:7,推出男生第2,3,4组体重数据的频率分别为0.15,0.25,0.35,男生第1,5,6组体重数据的频率.即可估计高一年段男生平均体重.
解答:
解:(Ⅰ)由男生体重数据频率分布直方图可知,体重落在区间[50,62)的频率为1-(0.025+0.025+0.0125)×4=0.75.
因为男生体重在[50,62)的人数为45,
所以本次抽样中男生抽取的总人数为45÷0.75=60.
因为样本是按性别分层抽样获取的,
所以根据饼形图描述的男,女生人数比,可知女生抽取的总人数为40.
所以体重落在区间[56,60]的女生人数为x=40-(2+18+10+5+3)=2.
(Ⅱ)体重落在区间[66,70]的男生人数为60×0.0125×4=3.
记体重落在[66,70]的3名男生为A,B,C,体重落在[56,60]的2名女生为a,b.
则事件“从体重在[66,70)的男生和体重在[56,60)的女生中选取2人进行复查”包含的基本事件有:(A,B),(A,C),(B,C),(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),(a,b),总数为10.
记“男、女生各有一人被选中”的事件为R,则事件R包含的基本事件有:(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),共6个.
因为事件空间中基本事件个数有限,且每个基本事件发生的可能性相同,所以该概率模型属于古典概率模型,
所以男、女生各有一人被选中的概率P(A)=
=
.
(Ⅲ)因为体重在[50,54),[54,58),[58,62)的男生人数比为3:5:7,
又由(Ⅰ)可知体重落在区间[50,62)的频率为0.75,
所以男生第2,3,4组体重数据的频率分别为0.15,0.25,0.35.
因为由直方图可知,男生第1,5,6组体重数据的频率分别为0.1,0.1,0.05,
所以样本中60名男生的平均体重约为:48×0.1+52×0.15+56×0.25+60×0.35+64×0.1+68×0.05=57.4.
以样本估计总体,可以估计高一年段男生平均体重为57.4公斤.
因为男生体重在[50,62)的人数为45,
所以本次抽样中男生抽取的总人数为45÷0.75=60.
因为样本是按性别分层抽样获取的,
所以根据饼形图描述的男,女生人数比,可知女生抽取的总人数为40.
所以体重落在区间[56,60]的女生人数为x=40-(2+18+10+5+3)=2.
(Ⅱ)体重落在区间[66,70]的男生人数为60×0.0125×4=3.
记体重落在[66,70]的3名男生为A,B,C,体重落在[56,60]的2名女生为a,b.
则事件“从体重在[66,70)的男生和体重在[56,60)的女生中选取2人进行复查”包含的基本事件有:(A,B),(A,C),(B,C),(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),(a,b),总数为10.
记“男、女生各有一人被选中”的事件为R,则事件R包含的基本事件有:(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),共6个.
因为事件空间中基本事件个数有限,且每个基本事件发生的可能性相同,所以该概率模型属于古典概率模型,
所以男、女生各有一人被选中的概率P(A)=
| 6 |
| 10 |
| 3 |
| 5 |
(Ⅲ)因为体重在[50,54),[54,58),[58,62)的男生人数比为3:5:7,
又由(Ⅰ)可知体重落在区间[50,62)的频率为0.75,
所以男生第2,3,4组体重数据的频率分别为0.15,0.25,0.35.
因为由直方图可知,男生第1,5,6组体重数据的频率分别为0.1,0.1,0.05,
所以样本中60名男生的平均体重约为:48×0.1+52×0.15+56×0.25+60×0.35+64×0.1+68×0.05=57.4.
以样本估计总体,可以估计高一年段男生平均体重为57.4公斤.
点评:本小题主要考查频率分布直方图、频率分布图表、古典概型、用频率估计概率的统计思想等统计与概率的基础知识,考查运算求解能力、数据处理能力、应用意识,考查必然与或然思想等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某校开设A类课3门,B类课5门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有
( )
( )
| A、15种 | B、30种 |
| C、45种 | D、90种 |
从1,2,3,4,5这5个数中任取两数,其中:①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个都是奇数;③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数. 上述事件中,是对立事件的是( )
| A、① | B、②④ | C、③ | D、①③ |
若函数f(x)=
+
,其中x∈[-
,a],若f(x)的值域是[-
,1],则a的取值范围是( )
| ||
| 2 |
| cos2x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.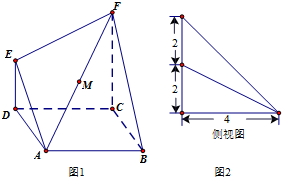 在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=
在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=