题目内容
有以下四个命题:
①对于任意实数a、b、c,若a>b,c≠0,则ac>bc;
②设Sn是等差数列{an}的前n项和,若a2+a6+a10为一个确定的常数,则S11也是一个确定的常数;
③在三角形△ABC中,若sinA>sinB,恒有A>B;
④对于任意正实数x,若sinx>0,y=sinx+
,则y的最小值为2
.
其中正确命题的是 (把正确的答案题号填在横线上)
①对于任意实数a、b、c,若a>b,c≠0,则ac>bc;
②设Sn是等差数列{an}的前n项和,若a2+a6+a10为一个确定的常数,则S11也是一个确定的常数;
③在三角形△ABC中,若sinA>sinB,恒有A>B;
④对于任意正实数x,若sinx>0,y=sinx+
| 2 |
| sinx |
| 2 |
其中正确命题的是
考点:命题的真假判断与应用
专题:综合题
分析:①根据不等式的基本性质可以判定命题①错误;
②等差数列{an}中,a2+a6+a10=k为常数时,可得a6为常数,即S11为常数,判定命题②正确;
③△ABC中,A>B等价于a>b,结合正弦定理
=
知,判定命题③正确;
④由|sinx|≤1,当sinx>0时,求出y=sinx+
的最小值,判定命题④错误.
②等差数列{an}中,a2+a6+a10=k为常数时,可得a6为常数,即S11为常数,判定命题②正确;
③△ABC中,A>B等价于a>b,结合正弦定理
| a |
| sinA |
| b |
| sinB |
④由|sinx|≤1,当sinx>0时,求出y=sinx+
| 2 |
| sinx |
解答:
解:对于①,根据不等式的基本性质得,
当c>0时,ac>bc,c<0时,ac<bc,∴命题①错误;
对于②,等差数列{an}中,设a2+a6+a10=k(k是常数),
∴a6=
,∴S11=11×
=
为常数,∴命题②正确;
对于③,△ABC中,A>B等价于a>b,
由正弦定理
=
知,若A>B,则a>b,∴sinA>sinB;
若sinA>sinB,则a>b,∴A>B;∴命题③正确;
对于④,∵|sinx|≤1,当sinx>0时,
y=sinx+
的最小值为1+2=3,∴命题④错误.
综上,正确的命题是②③.
故答案为:②③.
当c>0时,ac>bc,c<0时,ac<bc,∴命题①错误;
对于②,等差数列{an}中,设a2+a6+a10=k(k是常数),
∴a6=
| k |
| 3 |
| k |
| 3 |
| 11k |
| 3 |
对于③,△ABC中,A>B等价于a>b,
由正弦定理
| a |
| sinA |
| b |
| sinB |
若sinA>sinB,则a>b,∴A>B;∴命题③正确;
对于④,∵|sinx|≤1,当sinx>0时,
y=sinx+
| 2 |
| sinx |
综上,正确的命题是②③.
故答案为:②③.
点评:本题通过命题真假的判定,考查了不等式的基本性质,等差数列的应用,正弦定理的应用以及求函数的最小值等知识,是综合性题目.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
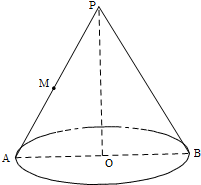 已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.
已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,底面半径OC与母线PB所成的角的大小等于θ.