题目内容
已知等差数列{an2}满足首项a12=1,且公差d=1,an>0,n∈N+.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=
,求数列{bn}的前项和Tn,并求lg(Tn+1)的取值范围.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=
| 1 |
| an+1+an |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)根据等差数列的通项公式先求出求{an2}的通项公式即可求数列{an}的通项公式;
(Ⅱ)求出bn=
的表达式,利用分母有理化进行化简求和即可.
(Ⅱ)求出bn=
| 1 |
| an+1+an |
解答:
解:(Ⅰ)∵等差数列{an2}满足首项a12=1,且公差d=1,
∴an2=a12+(n-1)d=n,
∵an>0,
∴an=
,
即数列{an}的通项公式an=
;
(Ⅱ)bn=
=
=
-
;
则数列{bn}的前项和Tn=
-1+
-
+…+
-
=
-1;
则lg(Tn+1)=lg(
-1+1)=lg
,
则lg(Tn+1)的取值范围为{m|m=lg
,n∈N•}
∴an2=a12+(n-1)d=n,
∵an>0,
∴an=
| n |
即数列{an}的通项公式an=
| n |
(Ⅱ)bn=
| 1 |
| an+1+an |
| 1 | ||||
|
| n+1 |
| n |
则数列{bn}的前项和Tn=
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
| n+1 |
则lg(Tn+1)=lg(
| n+1 |
| n+1 |
则lg(Tn+1)的取值范围为{m|m=lg
| n+1 |
点评:本题主要考查等差数列的应用,以及数列求和,利用分母有理化进的方法是解决本题的关键.

练习册系列答案
相关题目
如图,已知直角三角形ACB中,∠C=90°,D为AC上一点,且
=2
,∠ABD=30°,则cos∠ADB=( )
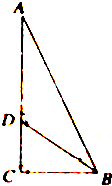
| AD |
| DC |

A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
若方程
=2x+m有实数解,则实数m的取值范围是( )
| x2-1 |
A、[-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
| D、(-∞,-2]∪[2,+∞) |
不等式|x-1|+|x+3|≤6的解集为( )
| A、[-4,2] |
| B、[2,+∞) |
| C、(-∞,-4] |
| D、(-∞,-4]∪[2,+∞) |

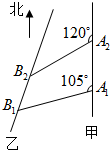 如图,甲船以每小时15
如图,甲船以每小时15