Question

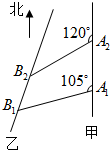如图，甲船以每小时15

2

海里的速度向正北方航行，乙船按固定方向匀速直线航行．当甲船位于A₁处时，乙船位于甲船的北偏西105°方向的B₁处，此时两船相距20海里；当甲船航行40分钟到达A₂处时，乙船航行到甲船的北偏西120°方向的B₂处，此时两船相距10

2

海里．问乙船每小时航行多少海里？

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：连接A₁B₂，依题意可知A₂B₂，求得A₁A₂的值，推断出△A₁A₂B₂是等边三角形，进而求得∠B₁A₁B₂，在△A₁B₂B₁中，利用余弦定理求得B₁B₂的值，即可求得乙船的速度．

解答： 解：如图，连结A₁B₂，由已知A2B2=10

2

，A1A2=15

2

×

40

60

=10

2

，…（2分）
∴A₁A₂=A₂B₂，
又∠A₁A₂B₂=180°-120°=60°，∴△A₁A₂B₂是等边三角形，…（4分）
∴A1B2=A1A2=10

2

，
由已知，A₁B₁=20，∠B₁A₁B₂=105°-60°=45°，…（6分）
在△A₁B₂B₁中，由余弦定理，B1

B

2 2

=A1

B

2 1

+A1

B

2 2

-2A1B1•A1B2•cos45°…（9分）=202+(10

2

)2-2×20×10

2

×

2

2

=200．
∴B1B2=10

2

．   …（12分）
因此，乙船的速度的大小为

10 2

40 60

=15

2

（海里/小时）．…（13分）
答：乙船每小时航行15

2

海里．  …（14分）

点评：本题主要考查了解三角形的实际应用．要能综合运用余弦定理，正弦定理等基础知识，考查了综合分析问题和解决实际问题的能力．