题目内容
15.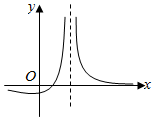 函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )
函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )| A. | a>0,b>0,c>0 | B. | a<0,b<0,c>0 | C. | a>0,b>0,c<0 | D. | a<0,b>0,c>0 |
分析 根据函数的定义域,极限,特殊值等方面判断.
解答 解:f(x)的定义域为{x|x≠c},结合函数图象可知c>0.
由图象可知f(0)<0,即$\frac{-b}{{c}^{2}}<0$,∴b>0.
∵当x>c时,f(x)>0,∴当x>c时,$\frac{ax-b}{(x-c)^{2}}>0$,即ax-b>0,∴a>$\frac{b}{x}>0$.
故选:A.
点评 本题考查了函数图象的判断,一般从函数图象的定义域,值域,单调性,特殊点等方面考虑.

练习册系列答案
相关题目
6.对于函数f(x),若存在常数a≠0,使得x取定义域内的每一个值,都有f(x)=-f(2a-x),则称f(x)为“准奇函数”.给定下列函数:①f(x)=$\sqrt{x}$;②f(x)=ex;③f(x)=cos(x+1);④f(x)=tanx.其中的“准奇函数”的有( )
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
10.设全集U={0,1,2},A={x|x2+ax+b=0},若∁UA={0,1},则实数a的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |