题目内容
20．用反证法证明“已知x＞y，证明：x3＞y3”假设的内容应是x3≤y3．分析 由于用反证法证明命题时，应先假设命题的否定成立，而“x3＞y3”的否定为：“x3≤y3”，由此得出结论．
解答 解：∵用反证法证明命题时，应先假设命题的否定成立，而“x3＞y3”的否定为：“x3≤y3”，
故答案为：x3≤y3
点评 本题主要考查用命题的否定，反证法证明数学命题的方法和步骤，把要证的结论进行否定，得到要证的结论的反面，是解题的突破口，属于中档题．
练习册系列答案
相关题目
15．
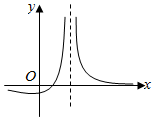函数f（x）=$\frac{ax-b}{{{{（x-c）}^2}}}$的图象如图所示，则下列结论成立的是（ ）
函数f（x）=$\frac{ax-b}{{{{（x-c）}^2}}}$的图象如图所示，则下列结论成立的是（ ）| A． | a＞0，b＞0，c＞0 | B． | a＜0，b＜0，c＞0 | C． | a＞0，b＞0，c＜0 | D． | a＜0，b＞0，c＞0 |
5．已知集合A={x∈R|-2＜x＜1}，B={x∈R|x2-2x＜0}，那么A∩B=（ ）
| A． | （-2，0） | B． | （-2，1） | C． | （0，2） | D． | （0，1） |
12．使“a＞b”成立的一个充分不必要条件是（ ）
| A． | a＞b+1 | B． | $\frac{a}{b}$＞1 | C． | a2＞b2 | D． | a3＞b3 |
9．已知函数f（x）是R上的偶函数，在（-3，-2）上为减函数且对?x∈R都有f（2-x）=f（x），若A，B是钝角三角形ABC的两个锐角，则（ ）
| A． | f（sinA）＜f（cosB） | B． | f（sinA）＞f（cosB） | ||
| C． | f（sinA）=f（cosB） | D． | f（sinA）与与f（cosB）的大小关系不确定 |
10．在△ABC中，a：b：c=3：2：4，则sinC=（ ）
| A． | -$\frac{1}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{\sqrt{15}}{4}$ | D． | -$\frac{\sqrt{15}}{4}$ |