题目内容
4.在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知曲线C1的极坐标方程为ρ=8$\sqrt{2}cos(θ-\frac{3π}{4})$,曲线C2的参数方程为$\left\{\begin{array}{l}x=8cosθ\\ y=3sinθ\end{array}\right.(θ$为参数).(Ⅰ)将曲线C1的极坐标方程化为直角坐标方程,将曲线C2的参数方程化为普通方程;
(Ⅱ)若P为C2上的动点,求点P到直线l:$\left\{\begin{array}{l}x=3+2t\\ y=-2+t\end{array}\right.(t$为参数)的距离的最小值.
分析 (Ⅰ)先利用两角和与差的三角函数化简极坐标方程,然后方程的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.消去参数求解参数方程的普通方程即可.
(Ⅱ)设P(8cosθ,3sinθ),求出直线的普通方程,利用点到直线的距离公式,通过两角和与差的三角函数,求解最值即可.
解答 解:(Ⅰ)由$ρ=8\sqrt{2}cos(θ-\frac{3π}{4})$得ρ=-8cosθ+8sinθ,
所以ρ2=-8ρcosθ+8ρsinθ,故曲线C1的直角坐标方程为x2+y2=-8x+8y,
即(x+4)2+(y-4)2=32,…(3分)
由$\left\{\begin{array}{l}x=8cosθ\\ y=3sinθ\end{array}\right.$消去参数θ得C2的普通方程为$\frac{x^2}{64}+\frac{y^2}{9}=1$.…(5分)
(Ⅱ)设P(8cosθ,3sinθ),直线l:$\left\{\begin{array}{l}x=3+2t\\ y=-2+t\end{array}\right.(t$为参数)的普通方程为x-2y-7=0,…(7分)
故点P到直线l的距离为$d=\frac{{\sqrt{5}}}{5}|{8cosθ-6sinθ-7}|=\frac{{\sqrt{5}}}{5}|{10cos(θ+φ)-7}|$(其中$cosφ=\frac{4}{5},sinφ=\frac{3}{5}$),
因此当$cos(θ+ϕ)=\frac{7}{10}$时,dmin=0,故点P到直线l的距离的最小值0.…(10分)
点评 本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.考查点到直线的距离公式的应用,两角和与差的三角函数的应用,考查计算能力.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案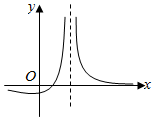 函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )
函数f(x)=$\frac{ax-b}{{{{(x-c)}^2}}}$的图象如图所示,则下列结论成立的是( )| A. | a>0,b>0,c>0 | B. | a<0,b<0,c>0 | C. | a>0,b>0,c<0 | D. | a<0,b>0,c>0 |
| A. | a>b+1 | B. | $\frac{a}{b}$>1 | C. | a2>b2 | D. | a3>b3 |
| A. | $({8\sqrt{3}-12,14}]$ | B. | $({8\sqrt{3}-12,8\sqrt{3}}]$ | C. | (12,14] | D. | (12,28] |
| A. | f(sinA)<f(cosB) | B. | f(sinA)>f(cosB) | ||
| C. | f(sinA)=f(cosB) | D. | f(sinA)与与f(cosB)的大小关系不确定 |

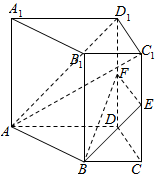 已知直四棱柱ABCD-A1B1C1D1,AD=DD1=2,BC=DC=1,DC⊥BC,AD∥BC,E,F分别为CC1,DD1的中点.
已知直四棱柱ABCD-A1B1C1D1,AD=DD1=2,BC=DC=1,DC⊥BC,AD∥BC,E,F分别为CC1,DD1的中点.