题目内容
4.已知向量$\overrightarrow a=(m,2)$,$\overrightarrow b=(-1,n)$,(n>0)且$\overrightarrow a•\overrightarrow b=0$,点P(m,n)在圆x2+y2=5上,则|2$\overrightarrow a+\overrightarrow b|$等于$\sqrt{34}$.分析 根据条件即可得到关于m,n方程组,这样由n>0便可解出m,n,从而得出向量的坐标,进而得出向量2$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,从而可求出向量的模.
解答 解:向量$\overrightarrow a=(m,2)$,$\overrightarrow b=(-1,n)$,(n>0)且$\overrightarrow a•\overrightarrow b=0$,
∴-m+2n=0,①
∴点P(m,n)在圆x2+y2=5上
∴m2+n2=5,②,
由①②可得m=2,n=1,
∴$\overrightarrow{a}$=(2,2)$\overrightarrow{b}$=(-1,1),
∴2$\overrightarrow{a}$+$\overrightarrow{b}$=(3,5),
∴|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{34}$,
故答案为:$\sqrt{34}$.
点评 考查向量数量积的坐标运算,曲线上点的坐标和曲线方程的关系,代入法解二元二次方程组,向量坐标的数乘和加法运算,根据向量坐标可求向量长度.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
15.已知集合A={x|x2-4x-12<0},B={x|2x>log${\;}_{\sqrt{3}}$3},则A∩B等于( )
| A. | ($\frac{3}{2},6$) | B. | ($\frac{3}{2},2$) | C. | (1,6) | D. | (1,2) |
12.在△ABC中,内角A,B,C的对边分别是a,b,c,若bsinB-asinA=$\frac{3}{2}asinC$,且△ABC的面积为a2sinB,则cosB等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
19.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
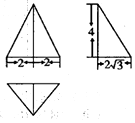
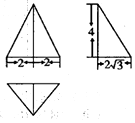
| A. | $\frac{{64\sqrt{3}}}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $\frac{32}{3}$ |
16.下列函数中,在(0,2)上为增函数的是( )
| A. | y=-3x+2 | B. | y=$\frac{3}{x}$ | C. | y=x2-4x+5 | D. | y=3x2+8x-10 |