题目内容
下列各组函数中，表示同一函数的是（ ）
A、y=
| ||||||
B、y=|x|与y=
| ||||||
C、y=x与y=
| ||||||
D、y=
|
考点：判断两个函数是否为同一函数
专题：函数的性质及应用
分析：根据函数的定义域相同、对应关系也相同，判定选项中的函数是否为同一函数．
解答：
解：A中，y=
•
的定义域是[2，+∞），y=
的定义域是（-∞，2]∪[2，+∞），∴不是同一函数；
B中，∵y=|x|=
，y=
=x，对应关系不同，∴不是同一函数；
C中，y=x，y=
=|x|=
，对应关系不同，∴不是同一函数；
D中，y=
=1（x≠0），y=x0=1（x≠0），它们的定义域相同，对应关系也相同，∴是同一函数；
故选：D．
| x+2 |
| x-2 |
| x2-4 |
B中，∵y=|x|=
|
| 3 | x3 |
C中，y=x，y=
| x2 |
|
D中，y=
| x |
| x |
故选：D．
点评：本题考查了根据函数的定义域、对应关系判定是否为同一函数的问题，是基础题．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
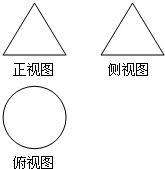如图所示，一个空间几何体的正视图和侧视图都是边长为2的等边三角形，俯视图是一个圆，那么这个几何体的体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线y2=4x上一点A的横坐标为4，则点A与抛物线焦点的距离为（ ）
| A、2 | B、3 | C、4 | D、5 |
已知集合A={x|-2≤x≤3}，B={x|-1≤x≤4}，那么集合A∩B等于（ ）
| A、{x|-2≤x≤4} |
| B、{x|3≤x≤4} |
| C、{x|-2≤x≤-1} |
| D、{x|-1≤x≤3} |
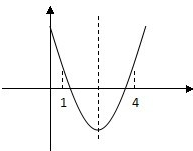已知关于x不等式x2-2ax+a+2≤0（a∈R）的解集为M．