题目内容
14.已知f(x)是定义在R上的减函数,其导函数f'(x)满足$\frac{f(x)+xf'(x)}{f'(x)}<1$,则下列结论中正确的是( )| A. | f(x)>0恒成立 | B. | f(x)<0 | ||
| C. | 当且仅当x∈(-∞,1),f(x)<0 | D. | 当且仅当x∈(1,+∞),f(x)>0 |
分析 令g(x)=(x-1)f(x),则g(x)在R递增,根据函数的单调性判断出f(x)的符号即可.
解答 解:∵$\frac{f(x)+xf'(x)}{f'(x)}<1$,f′(x)<0,
故f(x)+(x-1)f′(x)>0,
令g(x)=(x-1)f(x),则g(x)在R递增,
而g(1)=0,故x>1时,g(x)>0,x<1时,g(x)<0,则f(x)>0,
故f(x)>0在R恒成立,
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
9.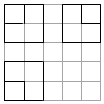 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
3.已知集合A={x|x2-x-2<0},$B=\left\{{x|{{log}_4}x<\frac{1}{2}}\right\}$,则( )
| A. | A∩B=∅ | B. | ∁UA∪B=R | C. | A∩B=B | D. | A∪B=B |
4.执行如图2所示的程序框图,若输出S=7,则输入k(k∈N*)的值为( )

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |