题目内容
13.在二分法求方程f(x)=0在[0,4]上的近似解时,最多经过12次计算精确度可以达到0.001.分析 精确度是方程近似解的一个重要指标,它由计算次数决定.若初始区间是(a,b),那么经过1次取中点后,区间的长度是$\frac{b-a}{2}$,…,经过n次取中点后,区间的长度是$\frac{b-a}{{2}^{n}}$,只要这个区间的长度小于精确度m,那么这个区间内的任意一个值都可以作为方程的近似解,由此可得结论.
解答 解:初始区间是[0,4],精确度要求是0.001,需要计算的次数n满足$\frac{5-1}{{2}^{n}}$<0.001,即2n>4000,
而210=1024,211=2048,212=4096>4000,故需要计算的次数是12.
故答案为:12
点评 本题考查二分法求方程的近似解,考查学生的计算能力,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
3.下列结论不正确的是( )
| A. | 若y=3,则y'=0 | B. | 若$y=\frac{1}{{\sqrt{x}}}$,则$y'=-\frac{{\sqrt{x}}}{2}$ | C. | 若$y=\sqrt{x}$,则$y'=\frac{1}{{2\sqrt{x}}}$ | D. | 若y=x,则y'=1 |
8.已知奇函数f(x)满足f(x+2)=f(x),当x∈(0,1)时,函数f(x)=2x,则$f({log_{\frac{1}{2}}}23)$=( )
| A. | $-\frac{16}{23}$ | B. | $-\frac{23}{16}$ | C. | $\frac{16}{23}$ | D. | $\frac{23}{16}$ |
2.$\sqrt{1-{{sin}^2}\frac{π}{5}}$的化简结果是( )
| A. | $cos\frac{π}{5}$ | B. | $-cos\frac{π}{5}$ | C. | $±cos\frac{π}{5}$ | D. | $sin\frac{π}{5}$ |
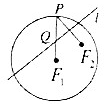 如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.
如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.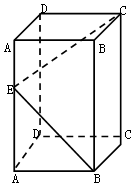 长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )
长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )