题目内容
3.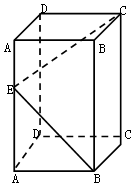 长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )
长方体ABCD-A1B1C1D1的底面是边长为2的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 设侧棱AA1的长为x,A1E=t,则AE=x-t,由已知得t2-xt+4=0,由此利用根的判别式能求出侧棱AA1的长的最小值.
解答 解:设侧棱AA1的长为x,A1E=t,则AE=x-t,
∵长方体ABCD-A1B1C1D1的底面是边长为2的正方形,
∠C1EB=90°,
∴$C{E}^{2}+B{E}^{2}=B{{C}_{1}}^{2}$,
∴8+t2+4+(x-t)2=4+x2,
整理,得:t2-xt+4=0,
∵在侧棱AA1上至少存在一点E,使得∠C1EB=90°,
∴△=(-x)2-16≥0,
解得x≥4.或x≤-4(舍).
∴侧棱AA1的长的最小值为4.
故选:B.
点评 本题考查长方体的侧棱长的最小值的求法,是中档题,解题时要注意根的判别式的合理运用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
18.已知复数$z=\frac{3}{1+i}$,则|z-1|为( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
8.已知向量$\vec n=(2,0,1)$为平面α的一个法向量,点A(-1,2,1)在α内,则P(1,2,-2)到平面α的距离为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{10}$ |
15.如图所示的程序的输出结果为S=1320,则判断框中应填( )
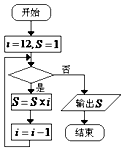

| A. | i≥9 | B. | i≤9 | C. | i≤10 | D. | i≥10 |
12.己知x0=-$\frac{π}{6}$是函数f(x)=sin(2x+φ)的一个极小值点,则f(x)的一个单调递减区间是( )
| A. | ($\frac{π}{3}$,$\frac{5π}{6}$) | B. | ($\frac{π}{6}$,$\frac{2π}{3}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{2π}{3}$,π) |
13.已知函数$f(x)={2016^x}+{log_{2016}}(\sqrt{{x^2}+1}+x)-{2016^{-x}}$+2,则关于x的不等式f(3x+1)+f(x)>4的解集为( )
| A. | (-$\frac{1}{2016}$,+∞) | B. | (-$\frac{1}{3}$,+∞) | C. | (-$\frac{1}{2}$,+∞) | D. | (-$\frac{1}{4}$,+∞) |
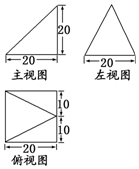 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.