题目内容
16.在直角坐标平面内,点A,B的坐标分别为(-1,0),(1,0),则满足tan∠PAB•tan∠PBA=m(m为非零常数)的点P的轨迹方程是( )| A. | ${x^2}-\frac{y^2}{m}=1(y≠0)$ | B. | ${x^2}-\frac{y^2}{m}=1$ | C. | ${x^2}+\frac{y^2}{m}=1(y≠0)$ | D. | ${x^2}+\frac{y^2}{m}=1$ |
分析 设P(x,y),则由题意,$\frac{y}{x+1}•(-\frac{y}{x-1})=m$(m≠0),化简可得结论.
解答 解:设P(x,y),则由题意,$\frac{y}{x+1}•(-\frac{y}{x-1})=m$(m≠0),
化简可得${x^2}+\frac{y^2}{m}=1(y≠0)$,
故选C.
点评 本题考查直接法求轨迹方程,考查斜率公式的运用,属于中档题.

练习册系列答案
相关题目
7.tan$\frac{π}{4}$等于( )
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
1.下列各式错误的是( )
| A. | 30.8>30.7 | B. | log0.50.4>log0.50.6 | ||
| C. | 0.75-0.1<0.750.1 | D. | log2$\sqrt{3}$>log3$\sqrt{2}$ |
8.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁UA)∪B为( )
| A. | {1,2,4} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
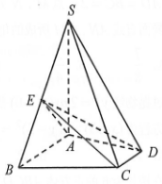 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.