题目内容
9.求不等式log3(2x+7)>log3(4x-1)中x的取值范围.分析 由对数函数的单调性化对数不等式为一元一次不等式组求解.
解答 解:原不等式化为$\left\{\begin{array}{l}{2x+7>0}\\{4x-1>0}\\{2x+7>4x-1}\end{array}\right.$,解得:$\frac{1}{4}$<x<4.
∴不等式log3(2x+7)>log3(4x-1)中x的取值范围是($\frac{1}{4},4$).
点评 本题考查对数不等式的解法,考查对数函数的单调性,是基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
4.在下列各函数中,偶函数是( )
| A. | y=x3 | B. | y=x4 | C. | y=$\sqrt{x}$ | D. | y=$\frac{1}{x}$ |

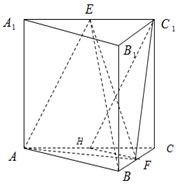 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.