题目内容
11．若方程x2+（m-3）x+m=0，m∈R，在x∈R上有两个不相等的实数根，求m的取值范围．分析 根据二次函数的性质求出m的范围即可．
解答 解：若方程x2+（m-3）x+m=0，m∈R，在x∈R上有两个不相等的实数根，
则△=（m-3）2-4m＞0，
解得：m＜1，或m＞9．
点评 本题考查了二次函数的性质，根据判别式求出m的范围即可．
练习册系列答案
相关题目
7．tan$\frac{π}{4}$等于（ ）
| A． | -1 | B． | 1 | C． | -$\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
8．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（∁UA）∪B为（ ）
| A． | {1，2，4} | B． | {2，3，4} | C． | {0，2，4} | D． | {0，2，3，4} |
3．设集合M={x|x2-3x-4≤0}，N={x||x-3|＜1}，则M∩N=（ ）
| A． | （2，4） | B． | （2，4] | C． | [2，4] | D． | （-1，4] |
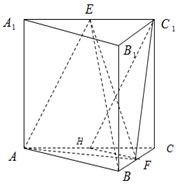如图，在三棱柱ABC-A1B1C1中，侧棱垂直于底面，AB=AC，E，F，H分别是A1C1，BC，AC的中点．