题目内容
2.已知函数f(x)=|x-a|,其中a>1.(1)当a=3时,求不等式f(x)≥4-|x-4|的解集;
(2)若函数h(x)=f(2x+a)-2f(x)的图象与x、y轴围成的三角形面积大于a+4,求a的取值范围.
分析 (1)写成分段函数的形式,对x讨论,结合一次不等式的解法,即可得到所求解集;
(2)记h(x)=f(2x+a)-2f(x),运用分段形式,求得h(x),由三角形的面积公式可得a2-2a-8>0,解不等式即可得到所求范围.
解答 解:(1)当a=3时,f(x)+|x-4|=$\left\{\begin{array}{l}{7-2x,x≤3}\\{1,3<x<4}\\{2x-7,x≥4}\end{array}\right.$,
当x≤3时,由f(x)≥4-|x-4|得,7-2x≥4,解得x≤$\frac{3}{2}$;
当3<x<4时,f(x)≥4-|x-4|无解;
当x≥4时,f(x)≥4-|x-4|得,2x-7≥4,解得x≥$\frac{11}{2}$.
∴f(x)≥4-|x-4|的解集为{x|x≤$\frac{3}{2}$或x≥$\frac{11}{2}$}.
(2)记h(x)=f(2x+a)-2f(x),
则h(x)=$\left\{\begin{array}{l}{-2a,x≤0}\\{4x-2a,0<x<a}\\{2a,x≥a}\end{array}\right.$,
所以S=$\frac{1}{2}$•2a•$\frac{a}{2}$>a+4,即为a2-2a-8>0,(a>1),
解得a>4.
即有a的取值范围为(4,+∞).
点评 本题考查绝对值不等式的解法,注意运用分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列函数中是偶函数的为( )
| A. | f(x)=|x-1| | B. | f(x)=cos(x-$\frac{π}{2}$) | C. | f(x)=0 | D. | f(x)=1+x2(x≥0) |
13.命题:“?x0∈R,x02+1>0或x0>sinx0”的否定是( )
| A. | ?x∈R,x2+1≤0且x≤sinx | B. | ?x∈R,x2+1≤0或x≤sinx | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$+1≤0且x0>sinx0 | D. | ?x0∈R,x${\;}_{0}^{2}$+1≤0或x0≤sinx0 |
17.某空间几何体的三视图如图所示,则该几何体的体积为( )
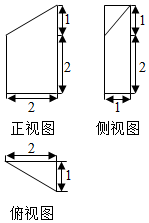

| A. | $\frac{8}{9}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{17}{3}$ |
