题目内容
17．某空间几何体的三视图如图所示，则该几何体的体积为（ ）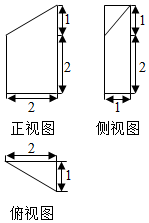
| A． | $\frac{8}{9}$ | B． | $\frac{8}{3}$ | C． | 3 | D． | $\frac{17}{3}$ |
分析 由三视图可知该几何体为是一个直三棱柱且上面截去一个三棱锥，由三视图求出对应的数据，利用柱体、锥体体积公式求值即可．
解答 解：根据三视图可知几何体是一个直三棱柱且上面截去一个三棱锥，
三棱柱的底面是一个直角三角形，两条直角边分别是1、2，侧棱长是3，
三棱锥的底面与三棱柱一样，高是1，
所以几何体的体积V=$\frac{1}{2}×1×2×3-\frac{1}{3}×\frac{1}{2}×1×2×1$=3-$\frac{1}{3}$=$\frac{8}{3}$，
故选：B．
点评 本题考查三视图求几何体的体积，考查空间想象能力，三视图正确复原几何体是解题的关键．
练习册系列答案
相关题目
10．函数y=sin2x-2sin2x+1的最大值为（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 3 | D． | $\sqrt{3}$ |
9．执行如图的程序框图，则输出的s=（ ）
| A． | $\frac{1}{16}$ | B． | -$\frac{1}{16}$ | C． | $\frac{1}{32}$ | D． | -$\frac{1}{32}$ |
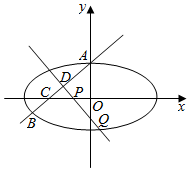已知椭圆$G：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的长轴长为4，离心率$e=\frac{{\sqrt{3}}}{2}$．