题目内容
11.若样本数据x1,x2,…,x10的平均数为8,则数据2x1-1,2x2-1,…,2x10-1的平均数为15.分析 根据平均数与方差的公式即可求出数据2x1-1,2x2-1,…,2x10-1的平均数.
解答 解:∵样本数据x1,x2,…,x10的平均数是10,
∴$\overline{x}$=$\frac{1}{10}$(x1+x2+…+x10)=8;
∴数据2x1-1,2x2-1,…,2x10-1的平均数是:
$\overline{x′}$=$\frac{1}{10}$[(2x1-1)+(2x2-1)+…+(2x10-1)]
=2×$\frac{1}{10}$(x1+x2+…+x10)-1=2×8-1=15.
故答案为:15.
点评 本题考查了计算数据的平均数问题,解题时应根据公式进行计算,也可以利用平均数的性质直接得出答案.

练习册系列答案
相关题目
1.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,x轴上有一点Q(2a,0),若C上存在一点P,使AP⊥PQ,则双曲线离心率的取值范围是( )
| A. | $e>\frac{{\sqrt{6}}}{2}$ | B. | $1<e<\frac{{\sqrt{6}}}{2}$ | C. | $e≥\frac{{\sqrt{6}}}{3}$ | D. | $1<e<\frac{{\sqrt{6}}}{3}$ |
19.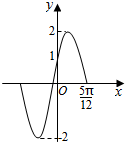 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
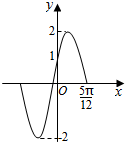 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )| A. | f($\frac{π}{3}$)=1 | |
| B. | 函数f(x)的图象关于x=$\frac{7π}{6}$对称 | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{2}$,0)对称 | |
| D. | 函数f(x)的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象 |
3.已知集合A={x|x2≥16},B={m},若A∪B=A,则实数m的取值范围是( )
| A. | (-∞,-4) | B. | [4,+∞) | C. | [-4,4] | D. | (-∞,-4]∪[4,+∞) |
20.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y≥0}\\{2x-y-4≤0}\end{array}\right.$,则目标函数z=2x+y的最大值为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
1.已知等差数列{an}公差为d,前n项和{sn},则下列描述不一定正确的是( )
| A. | 若a1>0,d>0,则n唯一确定时$s_n^{\;}$也唯一确定 | |
| B. | 若a1>0,d<0,则n唯一确定时$s_n^{\;}$也唯一确定 | |
| C. | 若a1>0,d>0,则$s_n^{\;}$唯一确定时n也唯一确定 | |
| D. | 若a1>0,d<0,则$s_n^{\;}$唯一确定时n也唯一确定 |
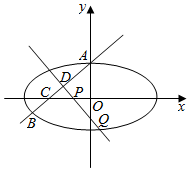 已知椭圆$G:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的长轴长为4,离心率$e=\frac{{\sqrt{3}}}{2}$.
已知椭圆$G:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的长轴长为4,离心率$e=\frac{{\sqrt{3}}}{2}$.