题目内容
15.已知平面α的一个法向量$\overrightarrow n=(0,-\frac{1}{2},-\sqrt{2})$,A∈α,P∉α,且$\overrightarrow{PA}=(-\frac{{\sqrt{3}}}{2},\frac{1}{2},\sqrt{2})$,则直线PA与平面α所成的角为$\frac{π}{3}$.分析 设直线PA与平面α所成的角为θ,则sinθ=|cosα|=$\frac{|\overrightarrow{n}•\overrightarrow{PA}|}{|\overline{n}||\overrightarrow{PA}|}$,即可得出.
解答 解:设直线PA与平面α所成的角为θ,则sinθ=|cosα|=$\frac{|\overrightarrow{n}•\overrightarrow{PA}|}{|\overline{n}||\overrightarrow{PA}|}$=$\frac{|0-\frac{1}{4}-2|}{\sqrt{0+\frac{1}{4}+2}\sqrt{\frac{3}{4}+\frac{1}{4}+2}}$=$\frac{\sqrt{3}}{2}$,
∴直线PA与平面α所成的角为$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了线面角的计算公式、数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.设集合A={x||x-2|≤2,x∈R},B={y|y=-x2,-1≤x≤2},则A∩B等于( )
| A. | R | B. | {0} | C. | {x|x∈R,x≠0} | D. | ∅ |
6.若复数z=$\frac{i}{-1+2i}$,则$\overline{z}$的虚部为( )
| A. | -$\frac{1}{5}$i | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$i | D. | $\frac{1}{5}$ |
3.直线2x+y+3=0在y轴上的截距是( )
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | 3 | D. | -3 |
7.若y=f(x)在(-∞,+∞)可导,且$\lim_{△x→0}\frac{f(a+2△x)-f(a)}{3△x}=1$,则f′(a)=( )
| A. | $\frac{2}{3}$ | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
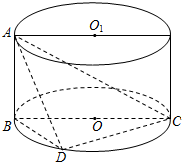 如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.
如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.