题目内容
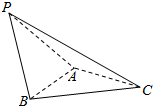 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.(Ⅰ)证明:AC=BC;
(Ⅱ)证明:AB⊥PC;
(Ⅲ)若PC=4,且平面PAC⊥平面PBC,求三棱锥P-ABC体积.
考点:棱柱、棱锥、棱台的体积,棱锥的结构特征
专题:计算题,空间位置关系与距离
分析:(Ⅰ)利用三角形全等可证;
(Ⅱ)先证AB⊥平面PDC,再由线面垂直的性质证明AB⊥PC;
(Ⅲ)作BE⊥PC,垂足为E,连结AE.证明∠AEB为二面角B-PC-A的平面角,求得三角形ABE的面积,根据VP-ABC=
×S△ABE×PC计算.
(Ⅱ)先证AB⊥平面PDC,再由线面垂直的性质证明AB⊥PC;
(Ⅲ)作BE⊥PC,垂足为E,连结AE.证明∠AEB为二面角B-PC-A的平面角,求得三角形ABE的面积,根据VP-ABC=
| 1 |
| 3 |
解答:
解:(Ⅰ)证明:∵△PAB是等边三角形,∠PAC=∠PBC=90°,
∴Rt△PBC≌Rt△PAC,可得AC=BC;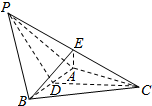
(Ⅱ)如图,取AB的中点D,连结PD,CD,
则PD⊥AB,CD⊥AB,
∴AB⊥平面PDC,PC?平面PDC,
∴AB⊥PC;
(Ⅲ)作BE⊥PC,垂足为E,连结AE.
∵△PAB是等边三角形,∴AE⊥PC,
同理BE⊥PC,∠AEB为二面角B-PC-A的平面角,且AE=BE.
∵平面PAC⊥平面PBC,∴∠AEB=90°.
∴△AEB,△PEB,△CEB都是等腰直角三角形.
又PC=4,得AE=BE=2,∴△AEB的面积S=2.
∵PC⊥平面AEB,
∴VP-ABC=
×2×4=
.
∴Rt△PBC≌Rt△PAC,可得AC=BC;

(Ⅱ)如图,取AB的中点D,连结PD,CD,
则PD⊥AB,CD⊥AB,
∴AB⊥平面PDC,PC?平面PDC,
∴AB⊥PC;
(Ⅲ)作BE⊥PC,垂足为E,连结AE.
∵△PAB是等边三角形,∴AE⊥PC,
同理BE⊥PC,∠AEB为二面角B-PC-A的平面角,且AE=BE.
∵平面PAC⊥平面PBC,∴∠AEB=90°.
∴△AEB,△PEB,△CEB都是等腰直角三角形.
又PC=4,得AE=BE=2,∴△AEB的面积S=2.
∵PC⊥平面AEB,
∴VP-ABC=
| 1 |
| 3 |
| 8 |
| 3 |
点评:本题考查了线面垂直的证明与性质,考查了棱锥的体积计算,考查了学生的推理论证能力及空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若PA=AB=BC=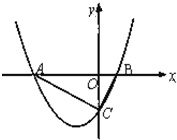 如图,已知抛物线
如图,已知抛物线 如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,D、E、F分别是PC、AC、BC的中点.
如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,D、E、F分别是PC、AC、BC的中点. (文科)如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
(文科)如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=