题目内容
18.已知在△ABC中,b(sinB+sinC)=(a-c)(sinA+sinC)(其中角A,B,C所对的边分别为a,b,c)且∠B为钝角.(1)求角A的大小;(2)若$a=\frac{{\sqrt{3}}}{2}$,求b+c的取值范围.
分析 (Ⅰ)由已知及正弦定理,余弦定理可求$cosA=-\frac{1}{2}$,结合范围A∈(0,π),可求A的值.
(Ⅱ)由正弦定理可知$2R=\frac{a}{sinA}=1$,利用三角函数恒等变换的应用化简可求b+c=$sin(C+\frac{π}{3})$,又0$<C<\frac{π}{3}$,可得范围$\frac{π}{3}$<C+$\frac{π}{3}$<$\frac{2π}{3}$,由正弦函数的图象和性质可求取值范围.(另可用均值不等式求解)
解答 解:(Ⅰ)由正弦定理得b(b-c)=(a+c)(a-c),…3分
可得:a2=b2+c2+bc,…4分
又a2=b2+c2-2bccosA,
于是$cosA=-\frac{1}{2}$,…5分
又A∈(0,π),
∴$A=\frac{2π}{3}$.…6分
(Ⅱ)∵$A=\frac{2π}{3}$,
∴$B+C=\frac{π}{3}$,且0$<C<\frac{π}{3}$,…7分
由正弦定理可知,$2R=\frac{a}{sinA}=1$,…8分
所以b+c=2RsinB+2RsinC=sinB+sinC,…9分
=$sin(\frac{π}{3}-C)+sinC$=$\frac{{\sqrt{3}}}{2}cosC-\frac{1}{2}sinC+sinC=\frac{1}{2}sinC+\frac{{\sqrt{3}}}{2}cosC$=$sin(C+\frac{π}{3})$,…10分
又0$<C<\frac{π}{3}$,可得:$\frac{π}{3}$<C+$\frac{π}{3}$<$\frac{2π}{3}$,
∴$b+c=sin(C+\frac{π}{3})$$∈({\frac{{\sqrt{3}}}{2},1}]$,…12分
注:用均值不等式求解更易,$由(1){a^2}={b^2}+{c^2}+bc及a=\frac{{\sqrt{3}}}{2}$,得:$\frac{3}{4}={b^2}+{c^2}+bc={(b+c)^2}-bc$,…6分
从而:$\frac{3}{4}={b^2}+{c^2}+bc={(b+c)^2}-bc≥{(b+c)^2}-{(\frac{b+c}{2})^2}$,…10分
∴b+c≤1,…11分
又$b+c>a=\frac{{\sqrt{3}}}{2}$,
∴$\frac{{\sqrt{3}}}{2}<b+c≤1$.…12分.
点评 本题主要考查了正弦定理,余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质,基本不等式在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | f(2)>e2f(0),f(2001)>e2001f(0) | B. | f(2)<e2f(0),f(2001)>e2001f(0) | ||
| C. | f(2)>e2f(0),f(2001)<e2001f(0) | D. | f(2)<e2f(0),f(2001)<e2001f(0) |
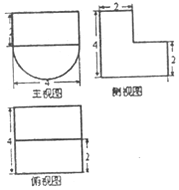
 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”外接球的体积为$\frac{8\sqrt{2}π}{3}$.
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”外接球的体积为$\frac{8\sqrt{2}π}{3}$.