题目内容
函数f（x）=
，若函数y=f（x）-2有3个零点，则实数a的值为 ．
|
考点：根的存在性及根的个数判断
专题：计算题,函数的性质及应用
分析：由题意知，当x≠4时，
=2仅有两个根，故当x=4时还有一个，从而解得．
| 2 |
| |x-4| |
解答：
解：当x≠4时，
=2，
解得，x=5，x=3；
又∵函数y=f（x）-2有3个零点，
则当x=4时，f（4）=a=2；
故答案为：2．
| 2 |
| |x-4| |
解得，x=5，x=3；
又∵函数y=f（x）-2有3个零点，
则当x=4时，f（4）=a=2；
故答案为：2．
点评：本题考查了函数的零点的应用，属于基础题．
练习册系列答案
相关题目
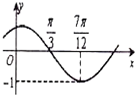函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
不论实数k取何值时，直线（k+1）x+（1-3k）y+2k-2=0恒过一定点，则该点的坐标是D（ ）
| A、（1，4） |
| B、（2，1） |
| C、（3，1） |
| D、（1，1） |
满足条件 {1，2}∪B={1，2，3，4，5}的所有集合B的个数为（ ）
| A、8 | B、4 | C、3 | D、2 |
若函数f（x）（x∈R）是奇函数，则（ ）
| A、函数f （x2）是奇函数 |
| B、函数[f （x）]2是奇函数 |
| C、函数f （x）•x2是奇函数 |
| D、函数f（x）+x2是奇函数 |
已知全集U=R，A={x|x＞-2}，B={x|x＞1}，则集合A∩（∁UB）=（ ）
| A、{x|-2＜x＜1} |
| B、{x|x≤1} |
| C、{x|-2＜x≤1} |
| D、{x|x＜-2} |