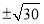题目内容
13.若x+2y=2$\sqrt{2a}$(x>0,y>0,a>1),则logax+logay的最大值是1.分析 利用基本不等式化简得出2$\sqrt{2a}$≥2$\sqrt{2xy}$,xy≤a,再利用对数函数单调性判断即可.
解答 解:∵x+2y=2$\sqrt{2a}$(x>0,y>0,a>1),
∴2$\sqrt{2a}$≥2$\sqrt{2xy}$,
xy≤a,
∴logax+logay=logaxy≤logaa=1,
故答案为:1.
点评 本题考察了基本不等式,对数函数的性质,在解决最大值,最小值中的应用,属于容易题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
5.在一次导弹实验中,为了确定爆炸点的位置,设立了A、B、C三个观测点.已知B在A的正西方向4a米处,C在A的正南方向a米处,实验中,在B,C两点听到导弹着地时的爆炸声比在A点分别晚2秒和1秒,且声速v=a米/秒,则此导弹爆炸点离A点的 距离为( )
| A. | a米 | B. | 2a米 | C. | 3a米 | D. | 4a米 |
18.已知过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点的直线1与C交于A,B两点,且使|AB|=4a的直线1恰好有3条,则双曲线C的渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
2.在△ABC中,B=$\frac{π}{3}$,AB=2,D为AB中点,△BCD的面积为$\frac{3\sqrt{3}}{4}$,则AC等于( )
| A. | 2 | B. | $\sqrt{7}$ | C. | $\sqrt{10}$ | D. | $\sqrt{19}$ |
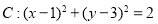 被直线
被直线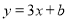 所截得的线段的长度等于2,则
所截得的线段的长度等于2,则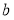 等于( )
等于( )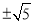 B.
B.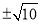 C.
C.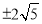 D.
D.