题目内容
5.在一次导弹实验中,为了确定爆炸点的位置,设立了A、B、C三个观测点.已知B在A的正西方向4a米处,C在A的正南方向a米处,实验中,在B,C两点听到导弹着地时的爆炸声比在A点分别晚2秒和1秒,且声速v=a米/秒,则此导弹爆炸点离A点的 距离为( )| A. | a米 | B. | 2a米 | C. | 3a米 | D. | 4a米 |
分析 以A,B所在的直线为x轴,AB的中点为原点,建立直角坐标系,可得A(2a,0),B(-2a,0),C(2a,-a),由题意可得|MB|-|MA|=2a<4a,运用双曲线的定义可得M的轨迹为右支,求得方程;再由|MC|-|MA|=a,可得M的轨迹为以A为端点的射线AM.求得方程为x=2a,(y>0),计算即可得到所求距离.
解答 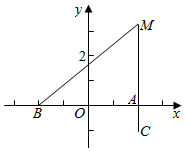 解:以A,B所在的直线为x轴,AB的中点为原点,建立直角坐标系,
解:以A,B所在的直线为x轴,AB的中点为原点,建立直角坐标系,
可得A(2a,0),B(-2a,0),C(2a,-a),
由题意可得|MB|-|MA|=2a<4a,
由双曲线的定义可得,M的轨迹为以A,B为焦点的双曲线的右支上一点.
可得双曲线的虚轴长为2$\sqrt{4{a}^{2}-{a}^{2}}$=2$\sqrt{3}$a,
方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3{a}^{2}}$=1①
又|MC|-|MA|=a,可得M的轨迹为以A为端点的射线AM.
方程为x=2a,(y>0),②
将②代入①可得,y=3a.
即有导弹爆炸点离A点的距离为3a.
故选:C.
点评 本题考查双曲线的定义和性质及应用,运用双曲线的定义是解题的关键,考查化简运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数f(x)=x2-4x+3( )
| A. | 在(-∞,2)内是减函数 | B. | 在(-∞,4)内是减函数 | ||
| C. | 在(-∞,0)内是减函数 | D. | 在(-∞,+∞)内是减函数 |