题目内容
9.已知线段BB′=4,直线l垂直平分BB′,交BB′于点O,在属于l并且以O为起点的同一射线上取两点P、P′,使OP•OP′=9,建立适当的坐标系,求直线BP与直线B′P′的交点M的轨迹方程.分析 由已知互相垂直的两条直线,以它建立直角坐标系,求出直线BP与B′P′的方程,找出交点M的M坐标,消掉字母即可得交点M的M轨迹方程.
解答 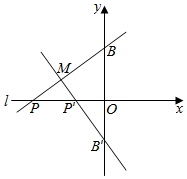 解:以O为原点,BB′为yy轴,l为xxx轴建立如图所示直角坐标系,则B(0,2),B′(0,-2),
解:以O为原点,BB′为yy轴,l为xxx轴建立如图所示直角坐标系,则B(0,2),B′(0,-2),
设P(a,0),a≠0,则由OP•OP′=9,得P′($\frac{9}{a}$,0),
直线BP的方程为$\frac{x}{a}+\frac{y}{2}=1$,即2x+ay-2a=0,
直线B′P′的方程为$\frac{x}{\frac{9}{a}}+\frac{y}{-2}=1$,即2ax-9y-18=0.
设M(x,y),联立$\left\{\begin{array}{l}{2x+ay-2a=0}\\{2ax-9y-18=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{18a}{{a}^{2}+9}}\\{y=\frac{2{a}^{2}-18}{{a}^{2}+9}}\end{array}\right.$,
消去a,可得4x2+9y2=36(x≠0).
∴点M的轨迹是长轴长为6,短轴长为4的椭圆(除去点B、B′).
点评 本题考查轨迹方程的求法,考查取的参数方程,联立方程组求解是关键,属中档题.

练习册系列答案
相关题目
 的顶点都在半径为
的顶点都在半径为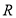 的球
的球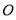 的球面上,且
的球面上,且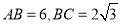 ,棱锥
,棱锥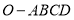 的体积为
的体积为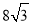 ,则
,则