题目内容
18.已知过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点的直线1与C交于A,B两点,且使|AB|=4a的直线1恰好有3条,则双曲线C的渐近线方程为( )| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
分析 由|AB|=4a的直线1恰好有3条,由双曲线的对称性可得,必有一条与x轴垂直,另两条关于x轴对称,令x=c,代入双曲线方程,计算即可得到弦长,由渐近线方程即可得到所求.
解答 解:由|AB|=4a的直线1恰好有3条,
由双曲线的对称性可得,必有一条与x轴垂直,
另两条关于x轴对称,
令x=c,代入双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),可得
y=±b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=±$\frac{{b}^{2}}{a}$,
即有此时|AB|=$\frac{2{b}^{2}}{a}$=4a,
即为b=$\sqrt{2}$a,
即有双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即为y=±$\sqrt{2}$x.
故选:A.
点评 本题考查双曲线的渐近线方程的求法,注意运用双曲线的对称性,考查运算能力,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
10.已知点A,B,C在圆O:x2+y2=2上运动,且AB⊥BC,若点P的坐标为(1,1),则|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|的取值范围是( )
| A. | [0,4$\sqrt{2}$] | B. | [2,4] | C. | [2$\sqrt{2}$,4$\sqrt{2}$] | D. | [2$\sqrt{2}$,3$\sqrt{2}$] |
 与圆
与圆 相交于
相交于 两点,若
两点,若 ,则
,则 的取值范围是______.
的取值范围是______.
 B.
B. C.
C.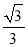 D.
D.