题目内容
5.已知a2+b2≥t(a+b-2)对a>1,b>1恒成立,则t的最大值为4.分析 利用基本不等式的性质即可得出.
解答 解:由a2+b2≥t(a+b-2)对a>1,b>1恒成立,
∴t≤$\frac{{a}^{2}+{b}^{2}}{a+b-2}$恒成立,
即t≤$\frac{(a-1+1)^{2}+(b-1+1)^{2}}{(a-1)+(b-1)}$=$\frac{(a-1)^{2}+(b-1)^{2}+2(a-1+b-1)+2}{(a-1)+(b-1)}$,
令x=a-1,y=b-1,x>0,y>0,
∴t≤$\frac{{x}^{2}+{y}^{2}+2(x+y)+2}{x+y}$=$\frac{{x}^{2}+{y}^{2}}{x+y}$+$\frac{2}{x+y}$+2恒成立,
只需要t≤($\frac{{x}^{2}+{y}^{2}}{x+y}$+$\frac{2}{x+y}$+2)min,
∵x2+y2≥2xy,
∴2(x2+y2)≥2xy+x2+y2=(x+y)2,
∴$\frac{{x}^{2}+{y}^{2}}{x+y}≥\frac{x+y}{2}$
∴$\frac{{x}^{2}+{y}^{2}}{x+y}$+$\frac{2}{x+y}$+2≥$\frac{x+y}{2}$+$\frac{2}{x+y}$+2≥2$\sqrt{\frac{2}{x+y}•\frac{x+y}{2}}$+2=4,
∴t≤4,
∴t的最大值为4,
故答案为:4.
点评 本题考查了基本不等式的应用,关键是换元和灵活变换,属于难题.

练习册系列答案
相关题目
20.设向量$\overrightarrow{a}$=($\sqrt{3}$,1),$\overrightarrow{b}$=(x,-3),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则向量$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
10.已知点A,B,C在圆O:x2+y2=2上运动,且AB⊥BC,若点P的坐标为(1,1),则|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|的取值范围是( )
| A. | [0,4$\sqrt{2}$] | B. | [2,4] | C. | [2$\sqrt{2}$,4$\sqrt{2}$] | D. | [2$\sqrt{2}$,3$\sqrt{2}$] |
14.函数f(x)=x2-4x+3( )
| A. | 在(-∞,2)内是减函数 | B. | 在(-∞,4)内是减函数 | ||
| C. | 在(-∞,0)内是减函数 | D. | 在(-∞,+∞)内是减函数 |
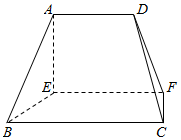 在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6.
在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6. 如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,求cosA=$\frac{\sqrt{6}}{4}$.
如图,在△ABC中,C=$\frac{π}{3}$,BC=4,点D在边AC上,AD=DB,DE⊥AB,E为垂足,若DE=2$\sqrt{2}$,求cosA=$\frac{\sqrt{6}}{4}$.