题目内容
17.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,过点P(3,6)的直线l与C相交于A,B两点,且AB的中点为N(12,15),则双曲线C的离心率为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
分析 方法一:由中点坐标公式,将A和B点代入双曲线的方程,两式相减即可求得直线的斜率,由直线AB的斜率k=$\frac{15-6}{12-3}$=1,即可求得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{5}{4}$,根据双曲线的离心率公式,即可求得双曲线C的离心率.
方法二:设A(12+m,15+n),B(12-m,15-n),代入双曲线方程,由直线l的斜率k=$\frac{n}{m}$=$\frac{4{b}^{2}}{5{a}^{2}}$,直线AB的斜率k=$\frac{15-6}{12-3}$=1,根据双曲线的离心率公式,即可求得双曲线C的离心率.
解答 解法一:设A(x1,y1),B(x2,y2),
由AB的中点为N(12,15),则x1+x2=24,y1+y2=30,
由$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{{a}^{2}}-\frac{{y}_{1}^{2}}{{b}^{2}}=1}\\{\frac{{x}_{2}^{2}}{{a}^{2}}-\frac{{y}_{2}^{2}}{{b}^{2}}=1}\end{array}\right.$,两式相减得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{{a}^{2}}$=$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{{b}^{2}}$,
则$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{{b}^{2}({x}_{1}+{x}_{2})}{{a}^{2}({y}_{1}+{y}_{2})}$=$\frac{4{b}^{2}}{5{a}^{2}}$,
由直线AB的斜率k=$\frac{15-6}{12-3}$=1,
∴$\frac{4{b}^{2}}{5{a}^{2}}$=1,则$\frac{{b}^{2}}{{a}^{2}}$=$\frac{5}{4}$,
双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{3}{2}$,
∴双曲线C的离心率为$\frac{3}{2}$,
故选B.
方法二:设A(12+m,15+n),B(12-m,15-n),
则$\left\{\begin{array}{l}{\frac{(12+m)^{2}}{{a}^{2}}-\frac{(15+n)^{2}}{{b}^{2}}=1}\\{\frac{(12-m)^{2}}{{a}^{2}}-\frac{(15-n)^{2}}{{b}^{2}}=1}\end{array}\right.$,两式相减得:$\frac{4m}{{a}^{2}}$=$\frac{5n}{{b}^{2}}$,
由直线l的斜率k=$\frac{n}{m}$=$\frac{4{b}^{2}}{5{a}^{2}}$,
直线AB的斜率k=$\frac{15-6}{12-3}$=1,
∴$\frac{4{b}^{2}}{5{a}^{2}}$=1,则$\frac{{b}^{2}}{{a}^{2}}$=$\frac{5}{4}$,
双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{3}{2}$,
∴双曲线C的离心率为$\frac{3}{2}$,
故选B.
点评 本题考查双曲线的离心率公式,考查中点坐标公式,考查点差法的应用,考查直线的斜率,考查计算能力,属于中档题.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案| A. | {x|-2≤x<0或3<x≤4} | B. | {x|-2≤x≤0或3≤x≤4} | C. | {x|-2<x≤4} | D. | {x|0<x<3} |
| A. | (0,$\frac{3}{4}$] | B. | (0,1] | C. | [$\frac{3}{4}$,1] | D. | [$\frac{3}{2}$,1] |
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 2 |
| E | 9500≤x<10500 | n |
(Ⅱ)记C组步数数据的平均数与方差分别为v1,$s_1^2$,E组步数数据的平均数与方差分别为v2,$s_2^2$,试分别比较v1与v2,$s_1^2$与$s_2^2$的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的步数数据中任取2个数据,求这2个数据步数差的绝对值大于3000步的概率.
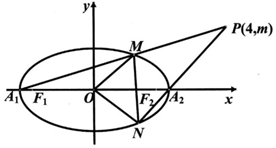 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.