执行如图的程序框图.若输出的y值为5.则判断框中可填入的条件是( )A．i＜3B．i＜4C．i＜5D．i＜6 题目和参考答案——青夏教育精英家教网——

题目内容

13．

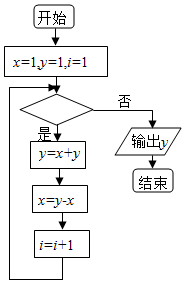执行如图的程序框图，若输出的y值为5，则判断框中可填入的条件是（　　）

A．

i＜3

B．

i＜4

C．

i＜5

D．

i＜6

分析根据程序框图，依次写出每次循环得到的运行结果，根据i=4时，退出循环，输出y的值为5，可得判断框内应填入的条件．

解答解：模拟执行程序，可得
x=1，y=1，i=1
满足条件，执行循环体，y=2，x=1，i=2
满足条件，执行循环体，y=3，x=2，i=3
满足条件，执行循环体，y=5，x=3，i=4
由题意，此时应该不满足条件，退出循环，输出y的值为5．
故判断框中可填入的条件是i≤3？或i＜4？．
故选：B．

点评本题主要考查了程序框图的应用，尤其考查循环结构，对循环体每次循环需要进行分析并找出内在规律，属基础题．

练习册系列答案

新天地阶梯阅读系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

相关题目

3．已知幂函数y=（m-1）²•x${\;}^{{m^2}-4m+2}}$在（0，+∞）上单调递增，则m的值为0．

4．已知长方体ABCD-A₁B₁C₁D₁中，AB=2，BC=BB₁=$\sqrt{2}$，在四边形ABC₁D₁内随机取一点M，则满足∠AMB≥135°的概率为（　　）

$\frac{π-2}{8}$

$\frac{2π-3\sqrt{3}}{12}$

$\frac{2\sqrt{2}-2}{8}$

1．若[x]表示不超过x的最大整数，执行如图所示的程序框图，则输出S的值为（　　）

8．给出下列命题：
①已知ξ服从正态分布N（0，δ²），且P（-2≤ξ≤2）=0.4，则P（ξ＞2）=0.3；
②函数f（x-1）是偶函数，且在（0，+∞）上单调递增，则f（2${\;}^{\frac{1}{8}}$）＞f（log₂$\frac{1}{8}$）＞f[（$\frac{1}{8}$）²]
③已知直线l₁：ax+3y-1=0，l₂：x+by+1=0，则l₁⊥l₂的充要条件是$\frac{a}{b}$=-3，
其中正确命题的序号是①②（把你认为正确的序号都填上）．

18．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，以点F₂为圆心的圆与双曲线的渐近线相切，切点为P．若∠F₁PF₂=$\frac{2π}{3}$，则双曲线的离心率为（　　）

$\frac{{\sqrt{13}}}{3}$

$\frac{{\sqrt{21}}}{3}$

5．设双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点为F，过点F作x轴的垂线交两渐近线于点A，B两点，且与双曲线在第一象限的交点为P，设O为坐标原点，若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+u$\overrightarrow{OB}$（λ，μ∈R），λ²+u²=$\frac{5}{8}$，则双曲线的离心率为（　　）

$\frac{{2\sqrt{3}}}{3}$

$\frac{{3\sqrt{5}}}{5}$

$\frac{{3\sqrt{2}}}{2}$

2．求下列情况下的概率．
（1）在集合{-3，-2，-1，1，2，3}中随机取两个数，分别记为a，b，求使得方程x²+2ax-b²+π=0有实根的概率
（2）在区间[-π，π]内随机取两个数，分别记为a，b，求使得方程x²+2ax-b²+π=0有实根的概率．

3．在直二面角α-l-β中，线段AB的端点A，B分别在α，β内，且AB与α，β所成的角均为30°，则AB与l所成的角为（　　）