题目内容
4.已知长方体ABCD-A1B1C1D1中,AB=2,BC=BB1=$\sqrt{2}$,在四边形ABC1D1内随机取一点M,则满足∠AMB≥135°的概率为( )| A. | $\frac{π}{8}$ | B. | $\frac{π-2}{8}$ | C. | $\frac{2π-3\sqrt{3}}{12}$ | D. | $\frac{2\sqrt{2}-2}{8}$ |
分析 由题意通过圆和三角形的知识确定满足条件的图形,分别找出满足条件的点集对应的图形面积,及图形的总面积,作比值即可.
解答  解:长方体ABCD-A1B1C1D1中,AB=2,BC=BB1=$\sqrt{2}$,
解:长方体ABCD-A1B1C1D1中,AB=2,BC=BB1=$\sqrt{2}$,
∴B1C1=2,
∴四边形ABC1D1为正方形,其面积为2×2=4,
以AB为底边,向正方形外作顶角为90°的等腰三角形,以等腰三角形的顶点O为圆心,OA为半径作圆,
根据圆周角相关定理,弧AB所对的圆周角为135°.即当M取圆O与ABC1D1的公共部分(弓形),∠AMB必大于135°
其中AB=2,OA=$\sqrt{2}$,
S阴影=$\frac{1}{4}$π($\sqrt{2}$)2-$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{2}$=$\frac{π}{2}$-1,
故所求的概率为$\frac{\frac{π}{2}-1}{4}$=$\frac{π-2}{8}$,
故选:B.
点评 本题考查几何概型的概率计算,关键是确定满足条件的区域,利用面积比值求解,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
14.执行如图所示程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
9.已知复数z满足(z+1)(1-i)=1+i,则复数z的共轭复数为( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
13.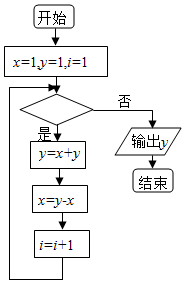 执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
 执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )| A. | i<3 | B. | i<4 | C. | i<5 | D. | i<6 |
