题目内容
18.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,以点F2为圆心的圆与双曲线的渐近线相切,切点为P.若∠F1PF2=$\frac{2π}{3}$,则双曲线的离心率为( )| A. | $\frac{{\sqrt{13}}}{3}$ | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{37}$ |
分析 根据渐近线和圆相切求出交点坐标,结合余弦定理以及双曲线的定义进行求解即可得到结论.
解答 解:∵点F2为圆心的圆与双曲线的渐近线相切,切点为P,
∴不妨设切线方程为y=$\frac{b}{a}$x,
F2P的方程为y=-$\frac{a}{b}$(x-c),
由$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{y=-\frac{a}{b}(x-c)}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{{a}^{2}}{c}}\\{y=\frac{ab}{c}}\end{array}\right.$,即P($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
则F1(-c,0),F2(c,0),
则|PF1|=$\sqrt{(\frac{{a}^{2}}{c}+c)^{2}+(\frac{ab}{c})^{2}}$=$\sqrt{3{a}^{2}+{c}^{2}}$,|PF2|=$\sqrt{(\frac{{a}^{2}}{c}-c)^{2}+(\frac{ab}{c})^{2}}$=$\sqrt{\frac{{b}^{4}}{{c}^{2}}+\frac{{a}^{2}{b}^{2}}{{c}^{2}}}$=$\sqrt{\frac{{b}^{2}({a}^{2}+{b}^{2})}{{c}^{2}}}$=b,
∵∠F1PF2=$\frac{2π}{3}$,
∴|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos$\frac{2π}{3}$,
即4c2=3a2+c2+b2+2$\sqrt{3{a}^{2}+{c}^{2}}$×b×$\frac{1}{2}$,
即3c2-3a2-b2=$\sqrt{3{a}^{2}+{c}^{2}}$×b,
即2b2=$\sqrt{3{a}^{2}+{c}^{2}}$×b,
则2b=$\sqrt{3{a}^{2}+{c}^{2}}$,
平方得4b2=3a2+c2,
即4(c2-a2)=3a2+c2,
整理得3c2=7a2,
则$\sqrt{3}$c=$\sqrt{7}$a,
则离心率e=$\frac{c}{a}$=$\frac{\sqrt{7}}{\sqrt{3}}$=$\frac{{\sqrt{21}}}{3}$,
故选:B.
点评 本题主要考查双曲线离心率的计算,根据渐近线和圆相切求出交点坐标,结合余弦定理进行求解是解决本题的关键.综合性较强,运算量较大.

| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $2\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{3}$ |
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
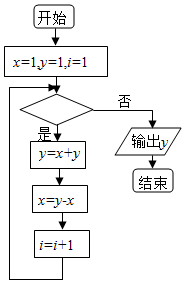 执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )| A. | i<3 | B. | i<4 | C. | i<5 | D. | i<6 |
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |

| A. | -12 | B. | 10 | C. | 16 | D. | 32 |
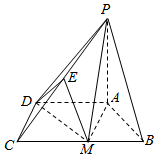 已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.
已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.