题目内容
2.求下列情况下的概率.(1)在集合{-3,-2,-1,1,2,3}中随机取两个数,分别记为a,b,求使得方程x2+2ax-b2+π=0有实根的概率
(2)在区间[-π,π]内随机取两个数,分别记为a,b,求使得方程x2+2ax-b2+π=0有实根的概率.
分析 (1)由题意知本题是一个古典概型,分别确定基本事件的个数,即可求使得方程x2+2ax-b2+π=0有实根的概率;
(2)由题意知本题是一个几何概型,由a,b使得函数f(x)=x2+2ax-b2+π有零点,得到关于a、b的关系式,写出试验发生时包含的所有事件和满足条件的事件,做出对应的面积,求比值得到结果.
解答 解:(1)由题意知本题是一个古典概型.
∵方程x2+2ax-b2+π=0有实根,
∴△=4a2+4b2-4π≥0,
∴a2+b2≥π,
在集合{-3,-2,-1,1,2,3}中随机取两个数,有A62=30种方法,满足a2+b2≥π有29种方法,
∴使得方程x2+2ax-b2+π=0有实根的概率为$\frac{29}{30}$;
(2)由题意知本题是一个几何概型,
∵a,b使得函数f(x)=x2+2ax-b2+π有零点,
∴△≥0
∴a2+b2≥π
试验发生时包含的所有事件是Ω={(a,b)|-π≤a≤π,-π≤b≤π}
∴S=4π2,
而满足条件的事件是{(a,b)|a2+b2≥π},
∴S=4π2-π2=3π2,
由几何概型公式得到P=$\frac{3}{4}$.
点评 本题考查概率的计算,考查古典概型、几何概型,考查学生的计算能力,正确区分两种概率类型是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.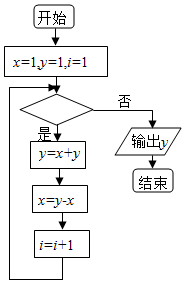 执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
 执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )| A. | i<3 | B. | i<4 | C. | i<5 | D. | i<6 |
10.执行如图所示的程序框图,输入p=10,则输出的A为( )


| A. | -12 | B. | 10 | C. | 16 | D. | 32 |
12.已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X>4)等于( )
(附:若随机变量ξ服从正态分布N(μ,σ2),且P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
(附:若随机变量ξ服从正态分布N(μ,σ2),且P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
| A. | 0.1588 | B. | 0.1587 | C. | 0.1586 | D. | 0.1585 |