题目内容
5.设双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,过点F作x轴的垂线交两渐近线于点A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+u$\overrightarrow{OB}$(λ,μ∈R),λ2+u2=$\frac{5}{8}$,则双曲线的离心率为( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{9}{8}$ |
分析 由方程可得渐近线,可得A,B,P的坐标,由已知向量式可得λ+μ=1,λ-μ=$\frac{b}{c}$,解之可得λμ的值,由λ2+u2=$\frac{5}{8}$,可得a,c的关系,由离心率的定义可得.
解答 解:双曲线的渐近线为:y=±$\frac{b}{a}$x,设焦点F(c,0),
则当x=c时,y═±$\frac{b}{a}$•c=±$\frac{bc}{a}$,
即A(c,$\frac{bc}{a}$),B(c,-$\frac{bc}{a}$),P(c,$\frac{{b}^{2}}{a}$),
因为$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,
所以(c,$\frac{{b}^{2}}{a}$)=((λ+μ)c,(λ-μ)$\frac{bc}{a}$),
所以λ+μ=1,λ-μ=$\frac{b}{c}$,
解得:λ=$\frac{c+b}{2c}$,μ=$\frac{c-b}{2c}$,
∵λ2+u2=$\frac{5}{8}$,
∴($\frac{c+b}{2c}$)2+($\frac{c-b}{2c}$)2=$\frac{5}{8}$,
即$\frac{2{c}^{2}+2{b}^{2}}{4{c}^{2}}$=$\frac{5}{8}$,
即c2=4b2.
则c2=4(c2-a2),
则3c2=4a2.
$\sqrt{3}$c=2a,
则e=$\frac{2}{\sqrt{3}}$=$\frac{{2\sqrt{3}}}{3}$,
故选:A.
点评 本题主要考查双曲线离心率的计算,根据交点坐标,结合平面向量的数量积公式是解决本题的关键.

练习册系列答案
相关题目
13.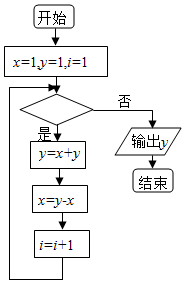 执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
 执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )
执行如图的程序框图,若输出的y值为5,则判断框中可填入的条件是( )| A. | i<3 | B. | i<4 | C. | i<5 | D. | i<6 |
20.已知z1=(m2+m+1)+(m2+m-4)i(m∈R),z2=3-2i,则“m=1”是“z1=z2”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | C. | 充要 | D. | 非充分非必要 |
10.执行如图所示的程序框图,输入p=10,则输出的A为( )


| A. | -12 | B. | 10 | C. | 16 | D. | 32 |
15.阅读如图所示的程序框图,当输出的结果S为0时,判断框中应填( )
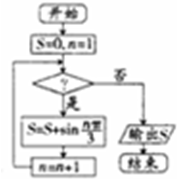

| A. | n≤4 | B. | n≤5 | C. | n≤7 | D. | n≤8 |