题目内容
 如图为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π )的图象的一部分,该函数的解析式是
如图为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π )的图象的一部分,该函数的解析式是考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由三角函数的图象直接得到A和T,代入周期公式求得ω,结合五点作图的第二点求得φ,则三角函数的解析式可求.
解答:
解:由图可得,A=2,T=2(
+
)=π,
∴ω=
=
=2,
由五点作图的第二点可得:2×(-
)+φ=
,解得:φ=
.
∴所求函数解析式为:y=2sin(2x+
).
故答案为:y=2sin(2x+
).
| 5π |
| 12 |
| π |
| 12 |
∴ω=
| 2π |
| T |
| 2π |
| π |
由五点作图的第二点可得:2×(-
| π |
| 12 |
| π |
| 2 |
| 2π |
| 3 |
∴所求函数解析式为:y=2sin(2x+
| 2π |
| 3 |
故答案为:y=2sin(2x+
| 2π |
| 3 |
点评:本题考查由y=Asin(ωx+φ)的部分图象求函数解析式,关键是掌握利用五点作图中的某一点求φ的值的方法,是基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
已知f(x)=f′(1)x2,则f′(0)等于( )
| A、0 | B、1 | C、2 | D、3 |
某几何体的三视图如图所示,则该几何体的体积是( )
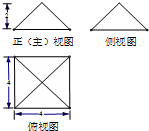

| A、32 | ||||
B、
| ||||
C、
| ||||
D、
|
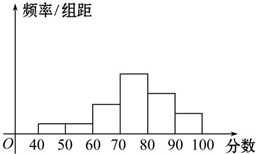 从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数
从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数