题目内容
已知二次函数f(x)=ax2+bx+c最小值为-1,且f(2-x)=f(2)+f(x).
(1)求f(x)的解析式;
(2)若f(x)在区间[2m,m+1]上单调,求m的取值范围.
(1)求f(x)的解析式;
(2)若f(x)在区间[2m,m+1]上单调,求m的取值范围.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)求出f(2-x),再由恒等式的性质,对应项的系数相等,即可得到f(x)=ax2-2ax,再由最小值为-1,即可得到a,进而得到解析式;
(2)求得对称轴,讨论区间和对称轴的关系,即可得到m的范围.
(2)求得对称轴,讨论区间和对称轴的关系,即可得到m的范围.
解答:
解:(1)f(2-x)=a(2-x)2+b(2-x)+c=ax2-(4a+b)x+4a+2b+c,
因为f(2-x)=f(2)+f(x)
所以ax2-(4a+b)x+4a+2b+c=4a+2b+c+ax2+bx+c,
即有
,即
所以f(x)=ax2-2ax=a(x-1)2-a,
因为f(x)=ax2+bx+c最小值为-1,所以a=1
所以f(x)=x2-2x;
(2)若f(x)在区间[2m,m+1]上单调,
所以
或
,即m≤0或
≤m<1
所以m的取值范围是(-∞,0]∪[
,1).
因为f(2-x)=f(2)+f(x)
所以ax2-(4a+b)x+4a+2b+c=4a+2b+c+ax2+bx+c,
即有
|
|
所以f(x)=ax2-2ax=a(x-1)2-a,
因为f(x)=ax2+bx+c最小值为-1,所以a=1
所以f(x)=x2-2x;
(2)若f(x)在区间[2m,m+1]上单调,
所以
|
|
| 1 |
| 2 |
所以m的取值范围是(-∞,0]∪[
| 1 |
| 2 |
点评:本题考查二次函数的解析式的求法,注意恒等式的性质,考查函数的单调性和运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
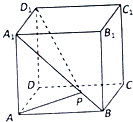 如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )
如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
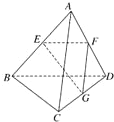 如图,已知空间四边形ABCD的每条边及AC、BD的长都为a,点E、F、G分别是AB、AD、DC的中点,求:
如图,已知空间四边形ABCD的每条边及AC、BD的长都为a,点E、F、G分别是AB、AD、DC的中点,求: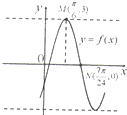 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<