题目内容
已知集合A={a,b,c,d},集合B={e,f},其中a,b,c,d,e,f均为实数.
(1)从集合A到集合B能构成多少个不同的映射?
(2)能构成多少个以集合A为定义域,集合B为值域的不同函数?
(1)从集合A到集合B能构成多少个不同的映射?
(2)能构成多少个以集合A为定义域,集合B为值域的不同函数?
考点:映射
专题:计算题,函数的性质及应用
分析:(1)要得到一个从集合A到集合B的映射,需要给A中的四个元素都在B中找到对应元素,分4步完成,每一步中都有2种找法,则从集合A到集合B能构成的映射个数为24;
(2)把(1)中的映射去掉像集为单元素集的即可得到以A为定义域,B为值域的不同的函数个数.
(2)把(1)中的映射去掉像集为单元素集的即可得到以A为定义域,B为值域的不同的函数个数.
解答:
解:(1)要“完成一个映射”可以分步完成:第一步a的像有2种可能,同理b,c,d的像也有2种可能,
∴A到B的映射共有2×2×2×2=24共16个;
(2)从A到B建立映射共有24=16个,其中有两个映射的像集为{1}和{-1},把这2个映射去掉,
∴构成以A为定义域,B为值域的不同的函数共有14个.
∴A到B的映射共有2×2×2×2=24共16个;
(2)从A到B建立映射共有24=16个,其中有两个映射的像集为{1}和{-1},把这2个映射去掉,
∴构成以A为定义域,B为值域的不同的函数共有14个.
点评:本题考查了映射与函数的概念,关键是对概念的理解,是基础题.

练习册系列答案
相关题目
若P是长度为6的线段AB上任意一点,则点P到线段AB两端距离均不小于1的概率( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中,其中是假命题的为( )
①若m,n是异面直线,且m⊥α,n⊥β,则α与β不会平行;
②函数f(x)=|cos2x-1|的最小正周期是π;
③命题“?a∈R,函数f(x)=(x-1)a+1恒过定点(1,1)”为真;
④“命题p∨q为真”是“命题p∧q为真”的必要不充分条件.
①若m,n是异面直线,且m⊥α,n⊥β,则α与β不会平行;
②函数f(x)=|cos2x-1|的最小正周期是π;
③命题“?a∈R,函数f(x)=(x-1)a+1恒过定点(1,1)”为真;
④“命题p∨q为真”是“命题p∧q为真”的必要不充分条件.
| A、0个 | B、1个 | C、2个 | D、3个 |
设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
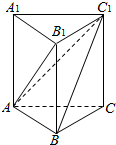 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=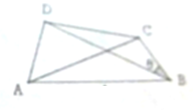 如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.
如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.