题目内容
等比数列{an}中,a1+a3=20,a2+a4=60,则a7+a8= .
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:由题意易得等比数列的公比q,再由通项公式可得.
解答:
解:设等比数列{an}的公比为q,
∵a1+a3=20,a2+a4=60,
∴q=
=
=3,
∴a7+a8=(a1+a3)q6=14580
故答案为:14580
∵a1+a3=20,a2+a4=60,
∴q=
| a2+a4 |
| a1+a3 |
| 60 |
| 20 |
∴a7+a8=(a1+a3)q6=14580
故答案为:14580
点评:本题考查等比数列的通项公式,求出数列的公比是解决问题的关键,属基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
下列函数中,在(-1,1)内有零点且单调递增的是( )
| A、y=log2x |
| B、y=2x-1 |
| C、y=x2-2 |
| D、y=-x3 |
已知i为虚数单位,则复数
等于( )
| 2 |
| 1-i |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
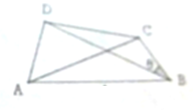 如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.
如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.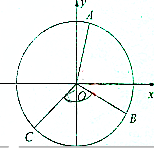 如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为
如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为