题目内容
3.已知函数f(x)=ax3-x+1的图象在点(1,f(1))处的切线过点(2,3).(1)求a的值;
(2)求函数f(x)的极值.
分析 (1)求出函数的导数,求出切线方程,得到关于a的方程,解出即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
解答 解:(1)∵f'(x)=3ax2-1,∴f'(1)=3a-1,
又f(1)=a,∴切线方程为y-a=(3a-1)(x-1),
∵切线过点(2,3),
∴3-a=3a-1,
解得a=1;
(2)由f(x)=3x2-1=0,
解得:${x_1}=-\frac{{\sqrt{3}}}{3},{x_2}=\frac{{\sqrt{3}}}{3}$,
x,f′(x),f(x)的变化如下:
| x | $({-∞,-\frac{{\sqrt{3}}}{3}})$ | $-\frac{{\sqrt{3}}}{3}$ | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | $\frac{{\sqrt{3}}}{3}$ | $({\frac{{\sqrt{3}}}{3},+∞})$ |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
f(x)的极大值为$f({-\frac{{\sqrt{3}}}{3}})=\frac{{4\sqrt{3}}}{3}+1$;
f(x)的极小值为$f({\frac{{\sqrt{3}}}{3}})=-\frac{{2\sqrt{3}}}{3}+1$.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
14.将函数y=sin2x的图象向右平移$\frac{π}{6}$个单位,得到函数y=f(x)的图象,则f(x)=( )
| A. | $cos(2x-\frac{π}{6})$ | B. | $sin(2x-\frac{π}{6})$ | C. | $cos(2x-\frac{π}{3})$ | D. | $sin(2x-\frac{π}{3})$ |
11.集合A={x|x2-2x-3≤0},B={x|x>2},A∩B=( )
| A. | [-1,3] | B. | (2,3] | C. | [-1,+∞) | D. | (2,+∞) |
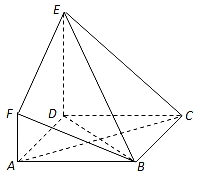 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.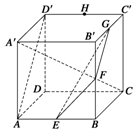 在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.
在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.