题目内容
8.已知函数$f(x)=\frac{(a-1)x+a}{{b{x^2}+c}}$(a,b,c为常数).(1)当b=1,c=0时,解关于x的不等式f(x)>1;
(2)当b=c>0,a=2时,若f(x)<1对于x>0恒成立,求实数b的取值范围.
分析 (1)当b=1,c=0时,化简f(x)>1,通过①当a<-1时,②当a=-1时,③当-1<a≤0时,④当a>0时,求出原不等式的解集即可.
(2)当b=c,a=2时,通过$f(x)<1?\frac{x+2}{{b{x^2}+b}}<1$,得到b的不等式,利用基本不等式求解即可.
解答 解:(1)当b=1,c=0时,f(x)>1?x2-(a-1)x-a<0(x≠0);
?(x-a)(x+1)<0讨论:①当a<-1时,原不等式的解集为(a,-1);
②当a=-1时,原不等式的解集为∅;
③当-1<a≤0时,原不等式的解集为(-1,a);
④当a>0时,原不等式的解集为(-1,0)∪(0,a).
(2)当b=c,a=2时,$f(x)<1?\frac{x+2}{{b{x^2}+b}}<1$,$?b>\frac{x+2}{{{x^2}+1}}(x>0)$;
令t=x+2,则$g(x)=\frac{x+2}{{{x^2}+1}}=\frac{t}{{{{(t-2)}^2}+1}}=\frac{1}{{t+\frac{5}{t}-4}}≤\frac{1}{{2\sqrt{5}-4}}=\frac{{\sqrt{5}}}{2}+1$;
当且仅当t=$\sqrt{5}$即x=$\sqrt{5}-2$时取等号.
故$b>\frac{{\sqrt{5}}}{2}+1$.
点评 本题考查函数的最值的求法,不等式的应用,基本不等式在最值中的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在空间直角坐标系O-xyz中,点(1,2,-2)关于点(-1,0,1)的对称点是( )
| A. | (-3,-2,4) | B. | (3,-2,-4) | C. | (-3,2,-4) | D. | (-3,2,4) |
20.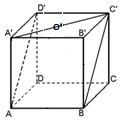 如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )
如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )
 如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )
如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
9.已知P是ABC所在平面内一点,$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\frac{3}{5}$$\overrightarrow{PA}$=$\overrightarrow{0}$,现将一粒黄豆随机撒在ABC内,则黄豆落在PBC内的概率是( )
| A. | $\frac{3}{13}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{10}{13}$ |
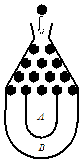 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.