题目内容
函数y=ax+4的图象与函数y=
的图象关于直线y=x对称,则logab+logba=( )
| x-b |
| 2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
考点:反函数
专题:函数的性质及应用
分析:由互为反函数图象间的关系求得a,b的值,代入logab+logba后由对数的运算性质求值.
解答:
解:y=ax+4的图象与函数y=
的图象关于直线y=x对称,说明两函数互为反函数,
由y=
,得x=2y+b,x,y互换后得函数y=
的反函数为y=2x+b,
∴a=2,b=4,
则logab+logba=log24+log42=2+
=
.
故选:A.
| x-b |
| 2 |
由y=
| x-b |
| 2 |
| x-b |
| 2 |
∴a=2,b=4,
则logab+logba=log24+log42=2+
| 1 |
| 2 |
| 5 |
| 2 |
故选:A.
点评:本题考查了反函数,考查了对数的运算性质,是基础题.

练习册系列答案
相关题目
在等差数列{an}中an>0,且a1+a2+a3+…+a8=40,则a4•a5的最大值是( )
| A、5 | B、10 |
| C、25 | D、AB=4,50 |
已知a、b、c是△ABC中A、B、C的对边,且a=1,b=5,c=2
,则△ABC的面积S=( )
| 5 |
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
已知(0.81.8)a>(1.80.8)a,则a的取值范围是( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
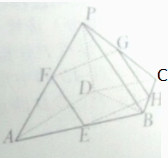 如图,在四棱锥P-ABCD中,若PD=4,DC=DB=3,PB=PC=5,AD⊥DB
如图,在四棱锥P-ABCD中,若PD=4,DC=DB=3,PB=PC=5,AD⊥DB