题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2},x>1}\\{\frac{1}{{2}^{x-1}},x≤1}\end{array}\right.$,则f(f($\sqrt{2}$))等于( )| A. | -3 | B. | $\frac{1}{8}$ | C. | 3 | D. | 8 |
分析 由已知得f($\sqrt{2}$)=-($\sqrt{2}$)2=-2,从而f(f($\sqrt{2}$))=f(-2),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{-{x}^{2},x>1}\\{\frac{1}{{2}^{x-1}},x≤1}\end{array}\right.$,
∴f($\sqrt{2}$)=-($\sqrt{2}$)2=-2,
f(f($\sqrt{2}$))=f(-2)=$\frac{1}{{2}^{-3}}$=8.
故选:D.
点评 本题考查函数值的求法,是基础题,解题时要 认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
15.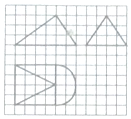 如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )
如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )
 如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )
如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )| A. | 16+4π | B. | 16+2π | C. | 48+4π | D. | 48+2π |
19.曲线f(x)=$\frac{1}{3}$x3-2在点(-1,f(-1))处切线的斜率为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
19.菱形ABCD中,E,F分别是AD,CD中点,若∠BAD=60°,AB=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
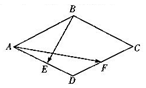

| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
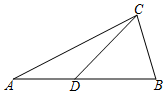 如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度):
如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度): 如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证:
如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证: