题目内容
10.已知直线l:(2m+1)x+(m+1)y-7m-4=0,圆C:(x-1)2+(y-1)2=25.(1)求证:直线l过定点;
(2)当m为何值时,直线l被圆C截得的弦最短.
分析 (1)把直线l的方程整理成m(2x+y-7)+(x+y-4)=0,由于m的任意性,有$\left\{\begin{array}{l}2x+y-7=0\\ x+y-4=0\end{array}\right.$,解此方程组,得直线l过定点;
(2)当直线l与DC垂直时,被截得的弦最短,即可得出结论.
解答 (1)证明:把直线l的方程整理成m(2x+y-7)+(x+y-4)=0
由于m的任意性,有$\left\{\begin{array}{l}2x+y-7=0\\ x+y-4=0\end{array}\right.$,解此方程组,得$\left\{\begin{array}{l}x=3\\ y=-1\end{array}\right.$,
所以直线l恒过定点D(3,1);
(2)解:当直线l与DC垂直时,被截得的弦最短,
此时,直线l与DC的斜率kl•kCD=-1,
由直线l的方程得${k_l}=-\frac{2m+1}{m+1}$,由点C、D的坐标得${k_{CD}}=\frac{2-1}{1-3}=-\frac{1}{2}$
∴$({-\frac{2m+1}{m+1}})•({-\frac{1}{2}})=-1$,解得$m=-\frac{3}{4}$,
所以,当$m=-\frac{3}{4}$时,直线l被圆C截得的弦最短.
点评 本题考查直线过定点的证明,考查直线与圆的位置关系,正确转化是关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
20.经过点M(2$\sqrt{6}$,-2$\sqrt{6}$)且与双曲线$\frac{y^2}{3}$-$\frac{x^2}{4}$=1有共同渐近线的双曲线方程为( )
| A. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{8}$=1 | B. | $\frac{{y}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{8}$=1 |
18.关于实数x,y的不等式组$\left\{\begin{array}{l}x≤4\\ y≥2\\ x-y+2≥0\end{array}\right.$所表示的平面区域记为M,不等式(x-4)2+(y-3)2≤1所表示的区域记为N,若在M内随机取一点,则该点取自N的概率为( )
| A. | $\frac{π}{16}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
5.已知i是虚数单位,复数z=m-1+(m+1)i,(其中m∈R)是纯虚数,则m=( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
15.已知椭圆方程2x2+3y2=1,则它的长轴长是( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
2.已知函数f(x)=ex-e-x+4sin3x+1,x∈(-1,1),若f(1-a)+f(1-a2)>2成立,则实数a的取值范围是( )
| A. | (-2,1) | B. | (0,1) | C. | $({1,\sqrt{2}})$ | D. | (-∞,-2)∪(1,+∞) |
20.已知双曲线$\frac{x^2}{m}+{y^2}=1$的离心率是$\sqrt{2}$,则实数m的值为( )
| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
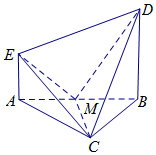 如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.
如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.