题目内容
9．（x+2y-$\frac{1}{z}$）6展开式中$\frac{x{y}^{2}}{{z}^{3}}$的系数为-240．分析 （x+2y-$\frac{1}{z}$）6展表示6个因式（x+2y-$\frac{1}{z}$）的乘积，故其中1个因式取x，2个因式取2y，剩下的3个因式取-$\frac{1}{z}$，可得展开式中含$\frac{x{y}^{2}}{{z}^{3}}$的项，根据乘法原理求得展开式中$\frac{x{y}^{2}}{{z}^{3}}$的系数．
解答 解：∵（x+2y-$\frac{1}{z}$）6展表示6个因式（x+2y-$\frac{1}{z}$）的乘积，
故其中1个因式取x，2个因式取2y，剩下的3个因式取-$\frac{1}{z}$，
可得展开式中含$\frac{x{y}^{2}}{{z}^{3}}$的项，
故展开式中$\frac{x{y}^{2}}{{z}^{3}}$的系数为${C}_{6}^{1}$•${C}_{5}^{2}$•22•（-1）=-240，
故答案为：-240．
点评 本题主要考查乘方的意义，乘法原理的运用，考查学生的计算能力，比较基础．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
20．经过点M（2$\sqrt{6}$，-2$\sqrt{6}$）且与双曲线$\frac{y^2}{3}$-$\frac{x^2}{4}$=1有共同渐近线的双曲线方程为（ ）
| A． | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{8}$=1 | B． | $\frac{{y}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | C． | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | D． | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{8}$=1 |
14．已知i是虚数单位，复数$z=i+\frac{2}{1-i}$，则复数$\overline z$的虚部是（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | $-\frac{3}{2}$ | D． | -2 |
18．关于实数x，y的不等式组$\left\{\begin{array}{l}x≤4\\ y≥2\\ x-y+2≥0\end{array}\right.$所表示的平面区域记为M，不等式（x-4）2+（y-3）2≤1所表示的区域记为N，若在M内随机取一点，则该点取自N的概率为（ ）
| A． | $\frac{π}{16}$ | B． | $\frac{π}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
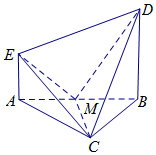如图，EA⊥平面ABC，DB⊥平面ABC，△ABC是等边三角形，AC=2AE，M是AB的中点．