题目内容
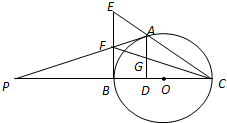 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.(1)求证:BF=EF;
(2)若PB=BC=3
| 2 |
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(1)利用平行线截三角形得相似三角形,得△BFC∽△DGC且△FEC∽△GAC,得到对应线段成比例,再结合已知条件可得BF=EF;
(2)利用直角三角形斜边上的中线的性质和等边对等角,得到∠FAO=∠EBO,结合BE是圆的切线,得到PA⊥OA,从而得到PA是圆O的切线,即可求出PA的长.
(2)利用直角三角形斜边上的中线的性质和等边对等角,得到∠FAO=∠EBO,结合BE是圆的切线,得到PA⊥OA,从而得到PA是圆O的切线,即可求出PA的长.
解答:
(1)证明:∵BC是圆O的直径,BE是圆O的切线,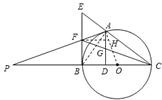
∴EB⊥BC,又∵AD⊥BC,∴AD∥BE,
∴△BFC∽△DGC,△FEC∽△GAC,∴
=
,
∵G是AD的中点,∴DG=AG,∴BF=EF;
(2)解:连结AO,AB.
∵BC是圆O的直径,∴∠BAC=90°,
在Rt△BAE中,由(1)知F是斜边BE的中点,
∴AF=FB=EF,∴∠FBA=∠FAB
又∵OA=OB,∴∠ABO=∠BAO,
∵BE是圆O的切线,∴∠EBO=90°,
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA是圆O的切线.
∴PA2=PB•PC=3
•6
=36,
∴PA=6.

∴EB⊥BC,又∵AD⊥BC,∴AD∥BE,
∴△BFC∽△DGC,△FEC∽△GAC,∴
| BF |
| DG |
| EF |
| AG |
∵G是AD的中点,∴DG=AG,∴BF=EF;
(2)解:连结AO,AB.
∵BC是圆O的直径,∴∠BAC=90°,
在Rt△BAE中,由(1)知F是斜边BE的中点,
∴AF=FB=EF,∴∠FBA=∠FAB
又∵OA=OB,∴∠ABO=∠BAO,
∵BE是圆O的切线,∴∠EBO=90°,
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA是圆O的切线.
∴PA2=PB•PC=3
| 2 |
| 2 |
∴PA=6.
点评:本题着重考查了直角三角形的性质、相似三角形的判定与性质和圆的切线判定定理等知识,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,已知AB是圆O的直径,圆O交BC于D,过点D作圆O的切线DE交AC于点E,且DE⊥AC.求证:AC=2OD.
如图,已知AB是圆O的直径,圆O交BC于D,过点D作圆O的切线DE交AC于点E,且DE⊥AC.求证:AC=2OD.