题目内容
已知Sn为等差数列{an}的前n项和,S6=51,a5=13.
(1)求数列{an}的通项公式;
(2)数列{bn}的通项公式是bn=2an,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)数列{bn}的通项公式是bn=2an,求数列{bn}的前n项和Sn.
考点:等比数列的前n项和,等比关系的确定
专题:计算题,等差数列与等比数列
分析:(1)设等差数列{an}的公差为d,利用S6=51,求出a1+a6=17,可得a2+a5=17,从而求出a2=4,可得公差,即可确定数列{an}的通项公式;
(2)求出数列{bn}的通项公式,利用等比数列的求和公式,可得结论.
(2)求出数列{bn}的通项公式,利用等比数列的求和公式,可得结论.
解答:
解:(1)设等差数列{an}的公差为d,则
∵S6=51,
∴
×6×(a1+a6)=51,
∴a1+a6=17,
∴a2+a5=17,
∵a5=13,∴a2=4,
∴d=3,
∴an=a2+3(n-2)=3n-2;
(2)bn=2an=-2•8n-1,
∴数列{bn}的前n项和Sn=
=
(8n-1).
∵S6=51,
∴
| 1 |
| 2 |
∴a1+a6=17,
∴a2+a5=17,
∵a5=13,∴a2=4,
∴d=3,
∴an=a2+3(n-2)=3n-2;
(2)bn=2an=-2•8n-1,
∴数列{bn}的前n项和Sn=
| 2(1-8n) |
| 1-8 |
| 2 |
| 7 |
点评:本题考查等差数列的通项公式与求和,考查等比数列的通项公式,确定等差数列的通项公式是关键.

练习册系列答案
相关题目
 如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,
如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,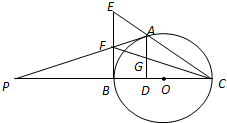 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.