题目内容
已知函数f(x)=x3+
+1,则满足不等式f(2m-1)+f(m)>2的实数m的取值范围 .
| 2x-1 |
| 2x+1 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据构造函数g(x)=f(x)-1,判断函数的奇偶性和单调性,将不等式进行转化即可得到结论.
解答:
解:∵f(x)=x3+
+1,
∴f(x)-1=x3+
,
设g(x)=f(x)-1=x3+
,
则g(-x)=-x3+
=-x3+
=-(x3+
)=-g(x),
则g(x)为奇函数,
又g(x)=f(x)-1=x3+
=x3+
=x3+1-
为增函数,
由f(2m-1)+f(m)>2,
得f(2m-1)-1+f(m)-1>0,
即g(2m-1)+g(m)>0,
则g(2m-1)>-g(m)=g(-m),
即2m-1>-m,
解得m>
,
故答案为:m>
| 2x-1 |
| 2x+1 |
∴f(x)-1=x3+
| 2x-1 |
| 2x+1 |
设g(x)=f(x)-1=x3+
| 2x-1 |
| 2x+1 |
则g(-x)=-x3+
| 2-x-1 |
| 2-x+1 |
| 1-2x |
| 1+2x |
| 2x-1 |
| 2x+1 |
则g(x)为奇函数,
又g(x)=f(x)-1=x3+
| 2x-1 |
| 2x+1 |
| 2x+1-2 |
| 2x+1 |
| 2 |
| 2x+1 |
由f(2m-1)+f(m)>2,
得f(2m-1)-1+f(m)-1>0,
即g(2m-1)+g(m)>0,
则g(2m-1)>-g(m)=g(-m),
即2m-1>-m,
解得m>
| 1 |
| 3 |
故答案为:m>
| 1 |
| 3 |
点评:本题主要考查不等式的求解,利用条件判断函数的奇偶性和单调性是解决本题的关键,综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=sin(wx+φ)(w>0,|φ|<
)的最小正周期是π,若将该函数的图象向右平移
个单位后得到的图象关于直线x=
对称,则函数f(x)的解析式为( )
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(2x+
| ||
D、f(x)=sin(2x-
|
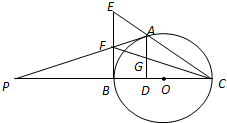 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P. 如图所示的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的全面积为
如图所示的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的全面积为